分析:分别根据线面平行的性质定理以及异面直线的定义,以及线面所成角的定义和计算分别进行判断.
解答:解:A.

设平面AD
1E与直线BC交于点G,连接AG、EG,则G为BC的中点
分别取B
1B、B
1C
1的中点M、N,连接AM、MN、AN,则
∵A
1M∥D
1E,A
1M?平面D
1AE,D
1E?平面D
1AE,
∴A
1M∥平面D
1AE.同理可得MN∥平面D
1AE,
∵A
1M、MN是平面A
1MN内的相交直线
∴平面A
1MN∥平面D
1AE,
由此结合A
1F∥平面D
1AE,可得直线A
1F?平面A
1MN,即点F是线段MN上上的动点.
∴A正确.
B.由A知,平面A
1MN∥平面D
1AE,
∴A
1F与D
1E不可能平行,∴B错误.
C.∵平面A
1MN∥平面D
1AE,BE和平面D
1AE相交,
∴A
1F与BE是异面直线,∴C正确.
D.设直线A
1F与平面BCC
1B
1所成角为θ
运动点F并加以观察,可知
当F与M(或N)重合时,A
1F与平面BCC
1B
1所成角等于∠A
1MB
1,此时所成角θ达到最小值,满足tanθ=
=2;
当F与MN中点重合时,A
1F与平面BCC
1B
1所成角达到最大值,满足tanθ=
=2∴A
1F与平面BCC
1B
1所成角的正切取值范围为[2,2
],即
tanθ≤2成立.
∴D正确.
故错误的是B.
故选:B.
点评:本题综合考查了空间直线和平面平行的位置关系的判断,以及异面直线和线面所成角的大小求法,综合性较强,计算量较大.

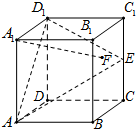 在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,记A1F与平面BCC1B1所成的角为θ,下列说法错误的是( )
在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,记A1F与平面BCC1B1所成的角为θ,下列说法错误的是( ) 设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点
设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点

 16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则 如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.
如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.