
为了某班学生喜爱打篮球是否与性别有关,对本班50人进行问卷调查得到了如下的列联表:

已知在全部50人中随机抽取1人,抽到不爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关;请说明理由.
附参考公式:
|
P( |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
k |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
解:∵已知在全部50人中随机抽取1人,抽到不爱打篮球的学生的概率为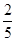
∴不爱打篮球的学生共有本质区别50×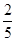 =20人
=20人
(1)列联表补充如下:
|
|
喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
男生 |
A+20 |
b=5 |
25 |
|
女生 |
c=10 |
d=15 |
25 |
|
合计 |
30 |
20 |
50 |
(2)∵
∴有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
【解析】本试题主要是考查了古典概型概率的求解和独立性检验的思想的运用。
(1)因为已知在全部50人中随机抽取1人,抽到不爱打篮球的学生的概率为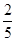 ,则可知结论。
,则可知结论。
(2)因为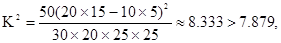 ,那么可以把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
,那么可以把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.


科目:高中数学 来源: 题型:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | a | b=5 | |
| 女生 | c=10 | d | |
| 合计 | 50 |
| 2 |
| 5 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P( K2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | a | b=5 | |
| 女生 | c=10 | d | |
| 合计 | 50 |
 .
.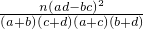 .
.| P( K2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:《统计》2013年高三数学一轮复习单元训练(浙江大学附中)(解析版) 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | a | b=5 | |
| 女生 | c=10 | d | |
| 合计 | 50 |
 .
. .
.| P( K2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com