
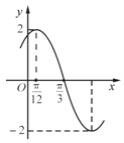
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() )的部分图象如图所示,下列说法正确的是( )
)的部分图象如图所示,下列说法正确的是( )
A. ![]() 的图象关于直线
的图象关于直线![]() 对称
对称
B. ![]() 的图象关于点
的图象关于点![]() 对称
对称
C. 将函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到函数
个单位得到函数![]() 的图象
的图象
D. 若方程![]() 在
在![]() 上有两个不相等的实数根,则实数
上有两个不相等的实数根,则实数![]() 的取值范围是
的取值范围是![]()
【答案】D
【解析】
由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出![]() 的值,可得函数的解析式,再结合正弦函数的图象和性质,得出结论.
的值,可得函数的解析式,再结合正弦函数的图象和性质,得出结论.
由函数的图象可得A=2,![]() ,求得ω=2.
,求得ω=2.
在根据五点法作图可得2![]() φ=π,求得φ
φ=π,求得φ![]() ,∴函数f(x)=2sin(2x
,∴函数f(x)=2sin(2x![]() ).
).
当![]() 时,f(x)=0,不是最值,故A不成立.
时,f(x)=0,不是最值,故A不成立.
当x![]() 时,f(x)=0=﹣2,不等于零,故B不成立.
时,f(x)=0=﹣2,不等于零,故B不成立.
将函数![]() 2sin(2x
2sin(2x![]() )的图象向左平移
)的图象向左平移![]() 个单位得到函数y=sin[2(x
个单位得到函数y=sin[2(x![]() )
)![]() ]=sin(2x
]=sin(2x![]() )的图象,故C不成立.
)的图象,故C不成立.
当x∈[![]() ,0]时,2x
,0]时,2x![]() ∈[
∈[![]() ,
,![]() ].
].
∵sin(![]() )=sin(
)=sin(![]() )
)![]() ,sin(
,sin(![]() )=﹣1,
)=﹣1,
故方程f(x)=m在![]() 上有两个不相等的实数根时,则m的取值范围是
上有两个不相等的实数根时,则m的取值范围是![]() ,故D成立;
,故D成立;
故选:D.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加 | 不准备参加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是双曲线
是双曲线![]() 上一点,
上一点, ![]() 分别是双曲线
分别是双曲线![]() 的左、右顶点,直线
的左、右顶点,直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求双曲线的离心率;
(2)过双曲线![]() 的右焦点且斜率为
的右焦点且斜率为![]() 的直线交双曲线于
的直线交双曲线于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() 为双曲线上一点,满足
为双曲线上一点,满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对![]() 名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝
名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝![]() 以上为“常喝”,体重超过
以上为“常喝”,体重超过![]() 为“肥胖”.
为“肥胖”.
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到肥胖的学生的概率为
人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
(3)已知常喝碳酸饮料且肥胖的学生中恰有2名女生,现从常喝碳酸饮料且肥胖的学生中随机抽取2人参加一个有关健康饮食的电视节目,求恰好抽到一名男生和一名女生的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com