
【题目】设双曲线![]() 的左焦点为
的左焦点为![]() ,点
,点![]() 为双曲线右支上的一点,且
为双曲线右支上的一点,且![]() 与圆
与圆![]() 相切于点
相切于点![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为坐标原点,则
为坐标原点,则![]() __________.
__________.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】学校射击队的某一选手射击一次,其命中环数的概率如表:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该选手射击一次,
(1)命中9环或10环的概率.
(2)至少命中8环的概率.
(3)命中不足8环的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 在第一象限内的点
在第一象限内的点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() .
.
(1)若![]() ,过点
,过点![]() ,
, ![]() 的直线
的直线![]() 与抛物线相交于另一点
与抛物线相交于另一点![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,与圆
两点,与圆![]() 相交于
相交于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得
,使得![]() 的长为定值?若存在,求出
的长为定值?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月,华中地区数城市空气污染指数“爆表”,此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:

(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为12万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,其中
,其中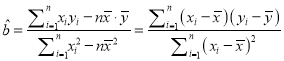 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=a(x-5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一装有水的直三棱柱ABC-A1B1C1容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面AA1B1B水平放置,如图所示,点D、E、F、G分别在棱CA、CB、C1B1、C1A1上,水面恰好过点D,E,F,C,且CD=2

(1)证明:DE∥AB;
(Ⅱ)若底面ABC水平放置时,求水面的高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某广场有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李,小王设计的底座形状分别为![]() ,
, ![]() ,经测量
,经测量![]() 米,
米, ![]() 米,
米, ![]() 米,
米, ![]()
(I)求![]() 的长度;
的长度;
(Ⅱ)若环境标志的底座每平方米造价为![]() 元,不考虑其他因素,小李,小王谁的设计建造费用最低(请说明理由),最低造价为多少?(
元,不考虑其他因素,小李,小王谁的设计建造费用最低(请说明理由),最低造价为多少?(![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,且满足
,且满足![]() .
.
(1)求点![]() 的轨迹方程所代表的曲线
的轨迹方程所代表的曲线![]() ;
;
(2)若点![]() ,
, ![]() ,
, ![]() 是曲线
是曲线![]() 上的动点,点
上的动点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() ,
, ![]() ,当点
,当点![]() 在
在![]() 上运动时,求点
上运动时,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 被直线
被直线![]() ,
, ![]() 分成面积相等的四个部分,且截
分成面积相等的四个部分,且截![]() 轴所得线段的长为2.
轴所得线段的长为2.
(1)求![]() 的方程;
的方程;
(2)若存在过点![]() 的直线与
的直线与![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰好是线段
恰好是线段![]() 的中点,求实数
的中点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com