已知定义在R上的函数f(x)和数列{an}满足下列条件:a1=a,a2≠a1,当n∈N*且n≥2时,an=f(an-1)且f(an)-f(an-1)=k(an-an-1).
其中a、k均为非零常数.
(1)若数列{an}是等差数列,求k的值;
(2)令bn=an+1-an(n∈N*),若b1=1,求数列{bn}的通项公式;
(3)试研究数列{an}为等比数列的条件,并证明你的结论.
解:(1)由已知a
n=f(a
n-1),f(a
n)-f(a
n-1)=k(a
n-a
n-1)(n=2,3,4,),得a
n+1-a
n=f(a
n)-f(a
n-1)=k(a
n-a
n-1)(n=2,3,4,)
由数列{a
n}是等差数列,得a
n+1-a
n=a
n-a
n-1(n=2,3,4,)
所以,a
n-a
n-1=k(a
n-a
n-1),(n=2,3,4,),得k=1.(5分)
(2)由b
1=a
2-a
1≠0,可得b
2=a
3-a
2=f(a
2)-f(a
1)=k(a
2-a
1)≠0.
且当n>2时,b
n=a
n+1-a
n=f(a
n)-f(a
n-1)=k(a
n-a
n-1)═k
n-1(a
2-a
1)≠0
所以,当n≥2时,
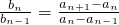
=
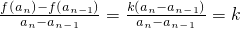
,(4分)
因此,数列{b
n}是一个公比为k的等比数列.(1分)
(3)解:{a
n}是等比数列的充要条件是f(x)=kx(k≠1)(2分)
充分性证明:
若f(x)=kx(k≠1),则由已知a
1=a≠0,a
n=f(a
n-1)(n=2,3,4,)得a
n=ka
n-1(n=2,3,4,)
所以,{a
n}是等比数列.(2分)
必要性证明:若{a
n}是等比数列,由(2)知,b
n=k
n-1(a
2-a
1)(n∈N
*)b
1+b
2++b
n-1=(a
2-a
1)+(a
2-a
1)++(a
n-a
n-1)=a
n-a
1(n≥2),a
n=a
1+(b
1+b
2++b
n-1).(1分)
当k=1时,a
n=a
1+(a
2-a
1)(n-1)(n≥2).
上式对n=1也成立,所以,数列{a
n}的通项公式为:a
n=a+(f(a)-a)(n-1)(n∈N
*).
所以,当k=1时,数列{a
n}是以a为首项,f(a)-a为公差的等差数列.
所以,k≠1.(1分)
当k≠1时,
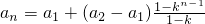
(n≥2).
上式对n=1也成立,所以,
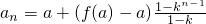
=
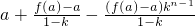
(1分)
所以,
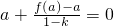
?f(a)=ka.(1分)
即,等式f(a)=ka对于任意实数a均成立.
所以,f(x)=kx(k≠1).(1分)
分析:(1)由题意知a
n=f(a
n-1),f(a
n)-f(a
n-1)=k(a
n-a
n-1)(n=2,3,4,),得a
n+1-a
n=f(a
n)-f(a
n-1)=k(a
n-a
n-1)(n=2,3,4,),由此可知a
n-a
n-1=k(a
n-a
n-1),(n=2,3,4,),得k=1.
(2)由b
1=a
2-a
1≠0,知b
2=a
3-a
2=f(a
2)-f(a
1)=k(a
2-a
1)≠0.因此b
n=a
n+1-a
n=f(a
n)-f(a
n-1)=k(a
n-a
n-1)═k
n-1(a
2-a
1)≠0,由此可知数列{b
n}是一个公比为k的等比数列.
(3){a
n}是等比数列的充要条件是f(x)=kx(k≠1);先进行充分性证明:若f(x)=kx(k≠1),则{a
n}是等比数列.再进行必要性证明:若{a
n}是等比数列,f(x)=kx(k≠1).
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

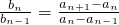 =
=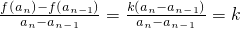 ,(4分)
,(4分)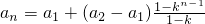 (n≥2).
(n≥2).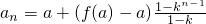 =
=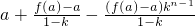 (1分)
(1分)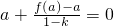 ?f(a)=ka.(1分)
?f(a)=ka.(1分)

 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案