
【题目】如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时, ![]() 的坐标为 .
的坐标为 . 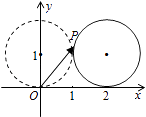
【答案】(2﹣sin2,1﹣cos2)
【解析】解:设滚动后的圆的圆心为O',切点为A(2,0),连接O'P,
过O'作与x轴正方向平行的射线,交圆O'于B(3,1),设∠BO'P=θ
∵⊙O'的方程为(x﹣2)2+(y﹣1)2=1,
∴根据圆的参数方程,得P的坐标为(2+cosθ,1+sinθ),
∵单位圆的圆心的初始位置在(0,1),圆滚动到圆心位于(2,1)
∴∠AO'P=2,可得θ= ![]() ﹣2
﹣2
可得cosθ=cos( ![]() ﹣2)=﹣sin2,sinθ=sin(
﹣2)=﹣sin2,sinθ=sin( ![]() ﹣2)=﹣cos2,
﹣2)=﹣cos2,
代入上面所得的式子,得到P的坐标为(2﹣sin2,1﹣cos2)
∴ ![]() 的坐标为(2﹣sin2,1﹣cos2).
的坐标为(2﹣sin2,1﹣cos2).
所以答案是:(2﹣sin2,1﹣cos2)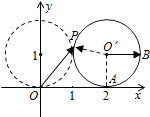
【考点精析】利用圆的参数方程对题目进行判断即可得到答案,需要熟知圆![]() 的参数方程可表示为
的参数方程可表示为![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(1-x)+lg(1+x)+x4-2x2.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高二学生![]() 、
、![]() 两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试![]() 、
、![]() 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2![]() 2列联表:
2列联表:
|
| 合计 | |
| 40 | 20 | 60 |
| 20 | 30 | 50 |
合计 | 60 | 50 | 110 |
(1)据此表格资料,能否在犯错的概率不超过0.01的前提下认为“![]() 学科合格”与“
学科合格”与“![]() 学科合格”有关;
学科合格”有关;
(2)从“![]() 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“![]() 学科合格”的人数为
学科合格”的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附公式与表:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,g(x)=ax2+bx(a,b∈R,a≠0)若y=f(x)的图象与y=g(x)图象有且仅有两个不同的公共点A(x1 , y1),B(x2 , y2),则下列判断正确的是( )
,g(x)=ax2+bx(a,b∈R,a≠0)若y=f(x)的图象与y=g(x)图象有且仅有两个不同的公共点A(x1 , y1),B(x2 , y2),则下列判断正确的是( )
A.当a<0时,x1+x2<0,y1+y2>0
B.当a<0时,x1+x2>0,y1+y2<0
C.当a>0时,x1+x2<0,y1+y2<0
D.当a>0时,x1+x2>0,y1+y2>0
查看答案和解析>>
科目:高中数学 来源: 题型:
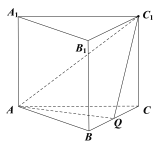
【题目】如图,在正三棱柱(底面为正三角形的直棱柱)ABC-A1B1C1中,已知AB=AA1=2,点Q为BC的中点.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面AQC1的距离.
到平面AQC1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2007全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩;
(2)分别计算两个样本的平均数![]() 和标准差
和标准差![]() ,并根据计算结果估计哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】行驶中的汽车,在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离,在某种路面上,某种型号的汽车的刹车距离s(m)与汽车的车速v(m/s)满足下列关系:![]() (n为常数,且
(n为常数,且![]() ),做了两次刹车实验,发现实验数据如图所示其中
),做了两次刹车实验,发现实验数据如图所示其中

(1)求出n的值;
(2)要使刹车距离不超过12.6米,则行驶的最大速度应为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地铁换乘站设有编号为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
安全出口编号 |
|
|
|
|
|
疏散乘客时间( | 186 | 125 | 160 | 175 | 145 |
则疏散乘客最快的一个安全出口的编号是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com