从1,2,3,…,9这九个数字中随机抽出数字,如依次抽取,抽后不放回,则抽到四个不同数字的概率是________;如依次抽取,抽后放回,则抽到四个不同数字的概率是________.
1 0.4601
分析:从九个数字中随机抽出数字,依次抽取,抽后不放回,则抽到四个不同数字是一个必然事件,得到概率是1,抽后放回,则抽到四个不同数字是一个等可能事件的概率,试验发生包含的事件是9
4,满足条件抽到四个不同数字有9×8×7×6,根据等可能事件的概率公式得到结果.
解答:从1,2,3,…,9这九个数字中随机抽出数字,依次抽取,
抽后不放回,则抽到四个不同数字是一个必然事件,
∴抽到不同数字的概率P=1,
如依次抽取,抽后放回,则抽到四个不同数字是一个等可能事件的概率,
试验发生包含的事件是9
4=6561,
满足条件抽到四个不同数字有9×8×7×6=3024
∴要求的概率是P=
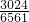
=0.4601
故答案为:1,0.4601
点评:本题考查判断事件的判断及事件发生概率的求法,考查必然事件的概率是1,考查等可能事件的概率求法公式,考查不放回抽样和放回抽样,是一个比较简单的综合题目.

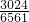 =0.4601
=0.4601
