
【题目】定义![]() ,已知函数
,已知函数![]() 、
、![]() 定义域都是
定义域都是![]() ,给出下列命题:
,给出下列命题:
(1)若![]() 、
、![]() 都是奇函数,则函数
都是奇函数,则函数![]() 为奇函数;
为奇函数;
(2)若![]() 、
、![]() 都是减函数,则函数
都是减函数,则函数![]() 为减函数;
为减函数;
(3)若![]() ,
,![]() ,则
,则![]() ;
;
(4)若![]() 、
、![]() 都是周期函数,则函数
都是周期函数,则函数![]() 是周期函数.
是周期函数.
其中正确命题的个数为( )
A.1个B.2个C.3个D.4个
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】![]() 是定义在区间
是定义在区间![]() 上且同时满足如下条件的函数
上且同时满足如下条件的函数![]() 所组成的集合:
所组成的集合:
①对任意的![]() ,都有
,都有![]() ;
;
②存在常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]()
(1)设![]() ,试判断
,试判断![]() 是否属于集合
是否属于集合![]() ;
;
(2)若![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,求证:满足条件的
,求证:满足条件的![]() 是唯一的;
是唯一的;
(3)设![]() ,且
,且![]() ,试求参数
,试求参数![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设计一个随机试验,使一个事件的概率与某个未知数有关,然后通过重复试验,以频率估计概率,即可求得未知数的近似解,这种随机试验在数学上称为随机模拟法,也称为蒙特卡洛法。比如要计算一个正方形内部不规则图形的面积,就可以利用撒豆子,计算出落在不规则图形内部和正方形内部的豆子数比近似等于不规则图形面积与正方形面积比,从而近似求出不规则图形的面积.
统计学上还有一个非常著名的蒲丰投针实验:平面上间隔![]() 的平行线,向平行线间的平面上任意投掷一枚长为
的平行线,向平行线间的平面上任意投掷一枚长为![]() 的针
的针![]() ,通过多次实验可以近似求出针与任一平行线(以
,通过多次实验可以近似求出针与任一平行线(以![]() 为例)相交(当针的中点在平行线外不算相交)的概率.以
为例)相交(当针的中点在平行线外不算相交)的概率.以![]() 表示针的中点与最近一条平行线
表示针的中点与最近一条平行线![]() 的距离,又以
的距离,又以![]() 表示
表示![]() 与
与![]() 所成夹角,如图甲,易知满足条件:
所成夹角,如图甲,易知满足条件:![]() ,
,![]() .
.
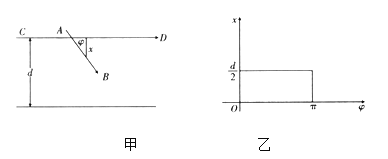
由这两式可以确定平面上的一个矩形![]() ,如图乙,在图甲中,当
,如图乙,在图甲中,当![]() 满足___________(
满足___________(![]() 与
与![]() ,
,![]() 之间的关系)时,针与平行线相交(记为事件
之间的关系)时,针与平行线相交(记为事件![]() ).可用从实验中获得的频率去近似
).可用从实验中获得的频率去近似![]() ,即投针
,即投针![]() 次,其中相交的次数为
次,其中相交的次数为![]() ,则
,则![]() ,历史上有一个数学家亲自做了这实验,他投掷的次数是5000,相交的次数为2550次,
,历史上有一个数学家亲自做了这实验,他投掷的次数是5000,相交的次数为2550次,![]() ,
,![]() ,依据这个实验求圆周率
,依据这个实验求圆周率![]() 的近似值_________.(精确到3位小数)
的近似值_________.(精确到3位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点为直角坐标系的原点,极轴为![]() 轴正半轴且单位长度相同的极坐标系中曲线
轴正半轴且单位长度相同的极坐标系中曲线![]() ,
,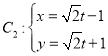 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 上的点到曲线
上的点到曲线![]() 距离的最小值;
距离的最小值;
(Ⅱ)若把![]() 上各点的横坐标都扩大原来为原来的2倍,纵坐标扩大原来的
上各点的横坐标都扩大原来为原来的2倍,纵坐标扩大原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设
,设![]() ,曲线
,曲线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com