
【题目】函数![]()
(1)讨论![]() 的单调性;
的单调性;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求证:
,求证: ![]()
【答案】(1) ![]() 时,
时, ![]() 在
在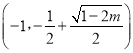 上单减,在
上单减,在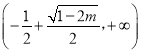 上单增;
上单增; ![]() 时,
时, ![]() 在
在 上单减,在
上单减,在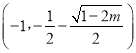 和
和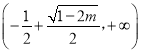 上单增;
上单增; ![]() 时,
时, ![]() 在
在![]() 上单增;(2)见解析.
上单增;(2)见解析.
【解析】试题分析:(1) ![]() ,分类讨论,研究
,分类讨论,研究![]() 的符号情况,进而得到函数的单调区间;(2) 设函数
的符号情况,进而得到函数的单调区间;(2) 设函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,
, ![]()
![]() 、
、![]() 是
是![]() 的二根
的二根![]()
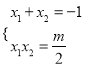 ,若证
,若证![]() 成立,只需证
成立,只需证![]() 对
对![]() 恒成立.设
恒成立.设![]() ,研究其最值即可.
,研究其最值即可.
试题解析:
解: ![]() 的定义域是
的定义域是![]() ,
,![]()
(1)由题设知, ![]()
令![]() ,这是开口向上,以
,这是开口向上,以![]() 为对称轴的抛物线.
为对称轴的抛物线.
在![]() 时,当
时,当![]() ,即
,即![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
②当![]() ,即
,即![]() 时,由
时,由![]() 得
得![]()
令![]() ,
, ![]()
则![]() ,
, ![]()
1) 当![]() 即
即![]() ,即
,即![]() 时,
时,
![]() 时,
时, ![]() ,即
,即![]() ,
, ![]() 时,
时, ![]() ,即
,即![]()
2) 当![]() 时,即
时,即![]() ,即
,即![]() 时
时
![]() 时,
时, ![]() ,即
,即![]()
![]() 或
或![]() 时,
时, ![]() ,即
,即![]()
综上:
![]() 时,
时, ![]() 在
在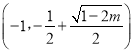 上单减,在
上单减,在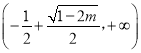 上单增;
上单增;
![]() 时,
时, ![]() 在
在 上单减,在
上单减,在 和
和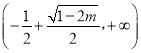 上单增;
上单增; ![]() 时,
时, ![]() 在
在![]() 上单增.
上单增.
(2)若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]()
则必是![]() ,则
,则![]() ,则
,则![]() ,
,
且![]() 在
在![]() 上单减,在
上单减,在![]() 和
和![]() 上单增,
上单增,
则![]()
![]()
![]() 、
、![]() 是
是![]() 的二根
的二根
![]()
 ,即
,即![]() ,
, ![]()
![]() 若证
若证![]() 成立,只需证
成立,只需证
![]()
![]()
![]()
即证![]() 对
对![]() 恒成立
恒成立
设![]()
![]()
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]()
故![]() ,故
,故![]() 在
在![]() 上单增
上单增
故![]()
![]()
![]() 对
对![]() 恒成立
恒成立
![]()
![]()


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() ,在以坐标原点为极点,
,在以坐标原点为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(Ⅰ)写出![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)点![]() ,
, ![]() 分别是曲线
分别是曲线![]() ,
, ![]() 上的动点,且点
上的动点,且点![]() 在
在![]() 轴的上侧,点
轴的上侧,点![]() 在
在![]() 轴的左侧,
轴的左侧, ![]() 与曲线
与曲线![]() 相切,求当
相切,求当![]() 最小时,直线
最小时,直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】超市某种绿色食品,过去20个月该食品的月市场需求量![]() (单位:
(单位: ![]() ,
, ![]() )即每月销售的数据记录如下:
)即每月销售的数据记录如下:
137 108 114 121 115 135 122 140 128 139
125 140 130 125 105 115 133 124 149 115
对这20个数据按组距10进行分组,并统计整理,绘制了如下尚不完整的统计图表:

(Ⅰ)写出![]() ,
, ![]() 的值.若视
的值.若视![]() 分布在各区间内的频率为相应的概率,试计算
分布在各区间内的频率为相应的概率,试计算![]() ;
;
(Ⅱ)记![]() 组月市场需求量数据的平均数与方差分别为
组月市场需求量数据的平均数与方差分别为![]() ,
, ![]() ,
, ![]() 组月市场需求量数据的平均数与方差分别为
组月市场需求量数据的平均数与方差分别为![]() ,
, ![]() ,试分别比较
,试分别比较![]() 与
与![]() ,
, ![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)为保证该绿色产品的质量,超市规定该产品仅在每月一日上架销售,每月最后一日对所有未售出的产品进行下架处理.若超市每售出![]() 该绿色食品可获利润5元,未售出的食品每
该绿色食品可获利润5元,未售出的食品每![]() 亏损3元,并且超市为下一个月采购了
亏损3元,并且超市为下一个月采购了![]() 该绿色食品,求超市下一个月销售该绿色食品的利润
该绿色食品,求超市下一个月销售该绿色食品的利润![]() 的分布列及数学期望
的分布列及数学期望![]() .(以分组的区间中点值代表该组的各个值,并以月市场需求量落入该区间的频率作为月市场需求量取该组区间中点值的概率)
.(以分组的区间中点值代表该组的各个值,并以月市场需求量落入该区间的频率作为月市场需求量取该组区间中点值的概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣5x﹣6<0},集合B={x|6x2﹣5x+1≥0},集合C={x|(x﹣m)(x﹣m﹣9)<0}
(1)求A∩B;
(2)若AC,求实数 m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC的中点,它的正(主)视图和侧(左)视图如图所示. 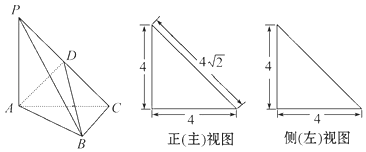
(Ⅰ)求三棱锥P﹣ABD的体积.
(Ⅱ)在∠ACB的平分线所在直线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com