
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)试在线段![]() 上找一点
上找一点![]() ,使
,使![]() 平面
平面![]() ,并说明理由.
,并说明理由.
【答案】(1)证明见解析;(2)![]() 为
为![]() 的中点.
的中点.
【解析】试题分析:(1)连接![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,又
,又![]() 满足线面垂直的判定定理,所以
满足线面垂直的判定定理,所以![]() 平面
平面![]() ,因为
,因为![]() 在面
在面![]() 内,所以可得
内,所以可得![]() ;(2)当
;(2)当![]() 为
为![]() 中点时,取
中点时,取![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,根据线面平行的判定定理可得
,根据线面平行的判定定理可得![]() 平面
平面![]() .
.
试题解析:(1)连接AC,过C作CE⊥AB,垂足为E
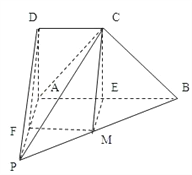
在四边形ABCD中,AD⊥AB,CD∥AB,AD=DC,
所以四边形ADCE是正方形.
所以∠ACD=∠ACE=45°,因为AE=CD=![]() AB,所以BE=AE=CE
AB,所以BE=AE=CE
所以∠BCE═45°所以∠ACB=∠ACE+∠BCE=90°
所以AC⊥BC,又因为BC⊥PC,AC∩PC=C,AC平面PAC,PC平面PAC/p>
所以BC⊥平面PAC,而PA平面PAC,所以PA⊥BC.
(2)当M为PB中点时,CM∥平面PAD,
证明:取AP中点为F,连接CM,FM,DF.则FM∥AB,FM=![]() AB,
AB,
因为CD∥AB,CD=![]() AB,所以FM∥CD,FM=CD. 所以四边形CDFM为平行四边形,所以CM∥DF,
AB,所以FM∥CD,FM=CD. 所以四边形CDFM为平行四边形,所以CM∥DF,
因为DF平面PAD,CM平面PAD,所以,CM∥平面PAD.
【方法点晴】本题主要考查线面平行的判定定理、线面垂直证明线线垂直,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(2)是就是利用方法①证明的.


科目:高中数学 来源: 题型:
【题目】设定义在(0,+∞)的单调函数f(x),对任意的x∈(0,+∞)都有f[f(x)﹣log2x]=6.若x0是方程f(x)﹣f′(x)=4的一个解,且 ![]() ,则a=( )
,则a=( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河北保定市高三上学期期末调研】如图,四面体![]() 中,
中, ![]() 、
、![]() 分别
分别![]() 、
、![]() 的中点,
的中点, ![]() ,
, ![]() .
.
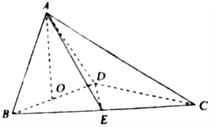
(I)求证: ![]() 平面
平面![]() ;
;
(II)求异面直线![]() 与
与![]() 所成角的余弦值的大小;
所成角的余弦值的大小;
(III)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个工厂生产某种产品的固定成本(固定投入)为![]() 元,已知每生产
元,已知每生产![]() 件这样的产品需要再增加成本
件这样的产品需要再增加成本![]() (元).已知生产出的产品都能以每件
(元).已知生产出的产品都能以每件![]() 元的价格售出.
元的价格售出.
(![]() )将该厂的利润
)将该厂的利润![]() (元)表示为产量
(元)表示为产量![]() (件)的函数.
(件)的函数.
(![]() )要使利润最大,该厂应生产多少件这样的产品?最大利润是多少?
)要使利润最大,该厂应生产多少件这样的产品?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为![]() ,右顶点为
,右顶点为![]() ,设点
,设点![]() .
.
(1)求该椭圆的标准方程;
(2)若![]() 是椭圆上的动点,求线段
是椭圆上的动点,求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2+bx+c(a≠0)经过点(﹣1,0),(0,0),(1,2).
(1)求f(x)的解析式;
(2)若数列{an}的前n项和Sn满足Sn=f(n),求{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一数学竞赛共设有35个考场,甲、乙、丙三所学校的领队各自将本校学生人数相同的考场归为一组.经统计,甲校共有i组,各组的考场数分别为![]() ;乙校共有j组,各组的考场数分别为
;乙校共有j组,各组的考场数分别为![]() ;丙校共有k组,各组的考场数分别为
;丙校共有k组,各组的考场数分别为![]() .已知
.已知![]() 包含了1 ~ 14的所有整数.证明:能找到三个考场,至少有两所学校在这三个考场中的选手人数各自是相同的.
包含了1 ~ 14的所有整数.证明:能找到三个考场,至少有两所学校在这三个考场中的选手人数各自是相同的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com