
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
分析 (1)根据图中数据,计算$\overline{x}$、$\overline{y}$,根据回归直线过样本中心点,求出a与y的值;
(2)根据题意,利用列举法求出基本事件数,计算对应的概率值即可.
解答 解:(1)根据图中数据,计算$\overline{x}$=$\frac{1}{5}$×(2+4+5+6+8)=5,
$\overline{y}$=$\frac{1}{5}$×(30+40+60+50+70)=50,
因为回归直线必过样本中心点$(\overline x,\overline y)$,
求得$a=\overline y-b\overline x=50-6.5×5=17.5$;
所以y=6.5x+17.5,
x=10时,y=6.5×10+17.5=82.5,
即估计y的预报值为82.5;
(2)易知原有的出油量不低于50L的井中,
3、5、6这3口井是优质井,2、4这2口井为非优质井,
由题意从这5口井中随机选取3口井的可能情况有:
(2,3.,4),(2,3,5),(2,3,6),(2,4,5),(2,4,6),
(2,5,6),(3,4,5),(3,4,6),(3,5,6),(4,5,6)共10种,
其中恰有2口是优质井的有6中,
所以所求概率是$P=\frac{6}{10}=\frac{3}{5}$.
点评 本题考查了线性回归方程的应用问题,也考查了利用列举法求古典概型的概率问题,是基础题目.


科目:高中数学 来源: 题型:解答题
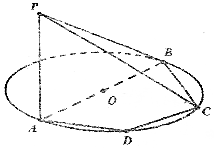 如图,PA⊥⊙O面,PA=2,AB为⊙O的直径,其长为4,四边形ABCD内接于圆O,且∠ADC=120°.
如图,PA⊥⊙O面,PA=2,AB为⊙O的直径,其长为4,四边形ABCD内接于圆O,且∠ADC=120°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=e-x-ex | B. | y=tanx | C. | y=x-3|x| | D. | y=ln(x+2)-ln(2-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com