
【题目】已知![]()
(1)若函数![]() 在区间
在区间![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围;
的取值范围;
(2)函数![]() 有几个零点?
有几个零点?
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
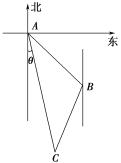
【题目】如图,甲船在A处,乙船在A处的南偏东45°方向,距A有9海里的B处,并以20海里每小时的速度沿南偏西15°方向行驶,若甲船沿南偏东θ度的方向,并以28海里每小时的速度行驶,恰能在C处追上乙船.问用多少小时追上乙船,并求sin θ的值.(结果保留根号,无需求近似值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名篮球运动员,甲投篮一次命中的概率为![]() ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为![]() ,若甲、乙各投篮三次,设
,若甲、乙各投篮三次,设![]() 为甲、乙投篮命中的次数的差的绝对值,其中甲、乙两人投篮是否命中相互没有影响.
为甲、乙投篮命中的次数的差的绝对值,其中甲、乙两人投篮是否命中相互没有影响.
(1)若甲、乙第一次投篮都命中,求甲获胜(甲投篮命中数比乙多)的概率;
(2)求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,
(如图一)的平面展开图(如图二)中,![]() 为边长等于
为边长等于![]() 的正方形,△
的正方形,△![]() 和△
和△![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中,
中,

(1)求证:![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
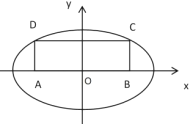
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() ,
,![]() 为焦点的椭圆
为焦点的椭圆![]() :
:![]() 恰好过
恰好过![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,直线
为原点,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 在
在![]() 轴异侧,若
轴异侧,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com