
【题目】(1)若![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的最大值
的最大值![]() ;
;
(2)在(1)的条件下,求证:函数![]() 在区间
在区间![]() 内存在唯一的极大值点
内存在唯一的极大值点![]() ,且
,且![]() .
.
【答案】(1)![]() .(2)家粘结性
.(2)家粘结性
【解析】
(1)令![]() ,求出导函数
,求出导函数![]() ,由
,由![]() 确定增区间,
确定增区间,![]() 确定减区间,从而得
确定减区间,从而得![]() 的最小值,得
的最小值,得![]() 的取值范围,即得
的取值范围,即得![]() ;
;
(2)求出导函数![]() ,通分后,令
,通分后,令![]() ,再求导数
,再求导数![]() ,令
,令![]() .分类讨论,当
.分类讨论,当![]() 时,
时,![]() ,得
,得![]() 递减,从而可得
递减,从而可得![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,
,![]() 时,令
时,令![]() .利用导数得
.利用导数得![]() 的单调性,从而得
的单调性,从而得![]() ,于是得出在
,于是得出在![]() 上
上![]() 的单调性,得唯一极大值点
的单调性,得唯一极大值点![]() .由
.由![]() 可对
可对![]() 变形,得
变形,得![]() ,只要证明在
,只要证明在![]() 上
上![]() ,从而可证得结论.
,从而可证得结论.
(1)解:令![]() ,则
,则![]() .
.
可见,![]() ;
;![]() .
.
故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以,当且仅当![]() 时,函数
时,函数![]() 取最小值1.
取最小值1.
由题意,实数![]() .所以
.所以![]() .
.
(2)由(1),![]() .
.
令![]() ,
,
则![]() .
.
令![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
可见,![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
又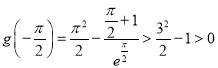 (由(1),可得
(由(1),可得![]() ,所以
,所以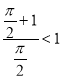 ),
),
![]() ,所以存在唯一的
,所以存在唯一的![]() ,使得
,使得![]() .
.
从而,当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减.
单调递减.
②当![]() 时,令
时,令![]() .
.
则![]() .所以
.所以![]() 在
在![]() 上单调递减.
上单调递减.
所以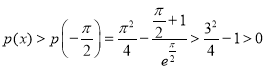 (由(1),可得
(由(1),可得![]() ,所以
,所以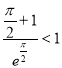 ).
).
又当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ,从而
,从而![]() .所以
.所以![]() 在
在![]() 单调递增.
单调递增.
综上所述,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单词递减.
上单词递减.
所以,函数![]() 在区间
在区间![]() 内存在唯一极大值点
内存在唯一极大值点![]() .
.
关于![]() 的证明如下:
的证明如下:
由上面的讨论,![]() ,且
,且![]() ,所以
,所以![]() ,所以
,所以![]() .
.
于是![]() .
.
令![]() .当
.当![]() 时,
时,![]() .所以
.所以![]() 在
在![]() 上单调递增.所以,当
上单调递增.所以,当![]() 时,
时,![]() ,即
,即![]() .
.
又因为![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() .
.
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.
(1)若![]() 过点
过点![]() ,且
,且![]() ,求
,求![]() 的斜率;
的斜率;
(2)若![]() ,且
,且![]() 的斜率为
的斜率为![]() ,当
,当![]() 时,求
时,求![]() 在
在![]() 轴上的截距的取值范围(用
轴上的截距的取值范围(用![]() 表示),并证明
表示),并证明![]() 的平分线始终与
的平分线始终与![]() 轴平行.
轴平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字![]() ,
,![]() ,
,![]() ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取![]() 次,每次抽取
次,每次抽取![]() 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求“抽取的卡片上的数字满足![]() ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字![]() ,
,![]() ,
,![]() 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() 、
、![]() 满足
满足![]() ,
,![]() .
.
(1)若数列![]() 是等比数列,试判断数列
是等比数列,试判断数列![]() 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(2)若![]() 恰好是一个等差数列的前
恰好是一个等差数列的前![]() 项和,求证:数列
项和,求证:数列![]() 是等差数列;
是等差数列;
(3)若数列![]() 是各项均为正数的等比数列,数列
是各项均为正数的等比数列,数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地网民浏览购物网站的情况,从该地随机抽取100名网民进行调查,其中男性、女性人数分别为60和40.下面是根据调查结果统计的数据,将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”,已知“网购达人”中女性人数为15人.
日均浏览购物网站时间(分钟) |
|
|
|
|
|
|
人数 | 2 | 14 | 24 | 35 | 20 | 5 |
(1)根据已知条件完成下面的![]() 列联表,并判断是否有99%的把握认为是否为“网购达人”与性别有关;
列联表,并判断是否有99%的把握认为是否为“网购达人”与性别有关;
非网购达人 | 网购达人 | 总计 | |
男 | |||
女 | 15 | ||
总计 |
(2)从上述调查中的“网购达人”中按性别分层抽样,抽取5人发放礼品,再从这5人中随机选出2人作为“最美网购达人”,求这两个“最美网购达人”中恰好为1男1女的概率.
参考公式: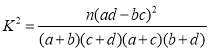 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
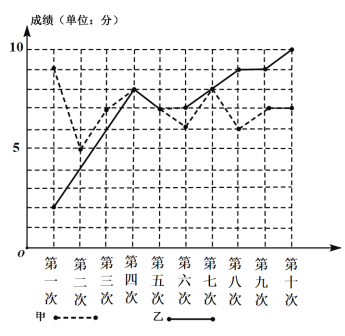
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com