
| A�� | 66 | B�� | 68 | C�� | 72 | D�� | 76 |
���� ��ͼ��ʾ��A��0��0����B��$4\sqrt{7}$��0������C��x��y����$\overrightarrow{BC}$=$��x-4\sqrt{7}��y��$������|$\overrightarrow{BC}$|=4=$\sqrt{��x-4\sqrt{7}��^{2}+{y}^{2}}$���ɵ�${y}^{2}=16-��x-4\sqrt{7}��^{2}$������$\overrightarrow{CP}$=3$\overrightarrow{PD}$��$\overrightarrow{CD}=\overrightarrow{AB}$=$��-4\sqrt{7}��0��$���ɵ�$\overrightarrow{AP}$=$\overrightarrow{AC}+\overrightarrow{CP}$��$\overrightarrow{BP}$=$\overrightarrow{AP}-\overrightarrow{AB}$���ɵ�$\overrightarrow{AP}•\overrightarrow{BP}$=-12=$��x-3\sqrt{7}����x-7\sqrt{7}��$+y2�����������ɵ�x�������ó���
���  �⣺��ͼ��ʾ��
�⣺��ͼ��ʾ��
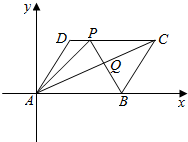
A��0��0����B��$4\sqrt{7}$��0����
��C��x��y����$\overrightarrow{BC}$=$��x-4\sqrt{7}��y��$��
��|$\overrightarrow{BC}$|=4=$\sqrt{��x-4\sqrt{7}��^{2}+{y}^{2}}$����Ϊ${y}^{2}=16-��x-4\sqrt{7}��^{2}$��
��$\overrightarrow{CP}$=3$\overrightarrow{PD}$��$\overrightarrow{CD}=\overrightarrow{AB}$=$��-4\sqrt{7}��0��$��
��$\overrightarrow{CP}$=$\frac{3}{4}\overrightarrow{AB}$=$��-3\sqrt{7}��0��$��
��$\overrightarrow{AP}$=$\overrightarrow{AC}+\overrightarrow{CP}$=$��x-3\sqrt{7}��y��$��
$\overrightarrow{BP}$=$\overrightarrow{AP}-\overrightarrow{AB}$=$��x-7\sqrt{7}��y��$��
��$\overrightarrow{AP}•\overrightarrow{BP}$=-12=$��x-3\sqrt{7}����x-7\sqrt{7}��$+y2����*��
��${y}^{2}=16-��x-4\sqrt{7}��^{2}$������ʽ����ɵã�
x=$\frac{9\sqrt{7}}{2}$��
��CD��AB��
��$\frac{AQ}{QC}=\frac{AB}{PC}=\frac{4}{3}$��
��$\overrightarrow{AQ}$=$\frac{4}{7}\overrightarrow{AC}$=$\frac{4}{7}$��x��y����
��$\overrightarrow{AB}•\overrightarrow{AQ}$=$\frac{16\sqrt{7}}{7}$x=$\frac{16\sqrt{7}}{7}��\frac{9\sqrt{7}}{2}$=72��
��ѡ��C��
���� ���⿼����ƽ���ı��ε����ʡ��������߶������������������ʡ����̵Ľⷨ�����������η�������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{2\sqrt{5}}{5}$��-$\frac{\sqrt{5}}{5}$�� | B�� | ��-$\frac{2\sqrt{5}}{5}$��$\frac{\sqrt{5}}{5}$�� | ||
| C�� | ��$\frac{\sqrt{5}}{5}$��-$\frac{2\sqrt{5}}{5}$����-$\frac{\sqrt{5}}{5}$��$\frac{2\sqrt{5}}{5}$�� | D�� | ��$\frac{2\sqrt{5}}{5}$��-$\frac{\sqrt{5}}{5}$����-$\frac{2\sqrt{5}}{5}$��$\frac{\sqrt{5}}{5}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com