
【题目】为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如下表:
与教育有关 | 与教育无关 | 合计 | |
男 | 30 | 10 | 40 |
女 | 35 | 5 | 40 |
合计 | 65 | 15 | 80 |
(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”?
参考公式:![]() (
(![]() ).
).
附表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
(2)求这80位师范类毕业生从事与教育有关工作的频率;
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
科目:高中数学 来源: 题型:
【题目】某车间生产某种产品,固定成本是![]() 万元,每生产
万元,每生产![]() 件产品成本增加
件产品成本增加![]() 元,根据经验,当年产量少于400件时,总收益
元,根据经验,当年产量少于400件时,总收益![]() (成本与总利润的和,单位:元)是年产量
(成本与总利润的和,单位:元)是年产量![]() (单位:件)的二次函数;,当年产量不少于
(单位:件)的二次函数;,当年产量不少于![]() 件时,R是Q的一次函数,以下是Q与R的部分数据:
件时,R是Q的一次函数,以下是Q与R的部分数据:
Q/ 件 | 50 | 200 | 350 | 500 | 650 |
R/ 元 | 23750 | 80000 | 113750 | 125000 | 1332500 |
问:每年生产多少件产品时,总利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为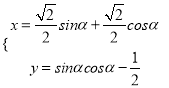 (
(![]() 为参数),若以直角坐标系中的原点为极点,
为参数),若以直角坐标系中的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为实数.)
为实数.)
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的极坐标方程为:
的极坐标方程为: ![]() .若以极点
.若以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求圆![]() 的直角坐标方程及其参数方程;
的直角坐标方程及其参数方程;
(Ⅱ)在直角坐标系中,点![]() 是圆
是圆![]() 上动点,求
上动点,求![]() 的最大值,并求出此时
的最大值,并求出此时
点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)= ![]() +alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
+alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
(1)求a的值.
(2)如果函数y=f(x)和函数y=g(x)在区间(b,b+1)上均为增函数,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种大型商品,A,B两地都有出售,且价格相同、某地居民从两地之一购得商品后运回的费用是:每单位距离A地的运费是B地的运费的3倍,已知A,B两地距离为10千米,顾客选择A或B地购买这种商品的标准是:包括运费和价格的总费用较低,求A,B两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购货地点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下2×2列联表:
喜欢数学课 | 不喜欢数学课 | 合计 | |
男 | 30 | 60 | 90 |
女 | 20 | 90 | 110 |
合计 | 50 | 150 | 200 |
经计算K2≈6.06,根据独立性检验的基本思想,约有(填百分数)的把握认为“性别与喜欢数学课之间有关系”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com