
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() ,
,![]() 实验地分别用甲、乙方法培训该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.
实验地分别用甲、乙方法培训该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.
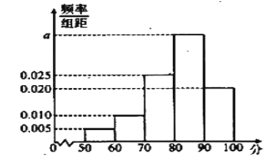
(1)求图中![]() 的值;
的值;
(2)填写下面的列联表,并判断是否有90%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: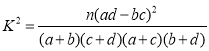 ,其中
,其中![]() .)
.)
科目:高中数学 来源: 题型:
【题目】下列关于充分必要条件的判断中,错误的是( )
A.“![]() ”是“
”是“![]() ”的充分条件
”的充分条件
B.“![]() ”是“
”是“![]() ”的必要条件
”的必要条件
C.“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
D.“![]() ,
,![]() ”是“
”是“![]() ”的非充分非必要条件
”的非充分非必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,经过
,经过![]() 轴正半轴上点
轴正半轴上点![]() 的直线
的直线![]() 交
交![]() 于不同的两点
于不同的两点![]() 和
和![]() .
.
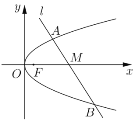
(1)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若![]() ,求证:原点
,求证:原点![]() 总在以线段
总在以线段![]() 为直径的圆的内部;
为直径的圆的内部;
(3)若![]() ,且直线
,且直线![]() ∥
∥![]() ,
,![]() 与
与![]() 有且只有一个公共点
有且只有一个公共点![]() ,问:△
,问:△![]() 的面积是否存在最小值?若存在,求出最小值,并求出
的面积是否存在最小值?若存在,求出最小值,并求出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省普通高中学业水平考试成绩按人数所占比例依次由高到低分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级,
五个等级,![]() 等级
等级![]() ,
,![]() 等级
等级![]() ,
,![]() 等级
等级![]() ,
,![]() ,
,![]() 等级共
等级共![]() .其中
.其中![]() 等级为不合格,原则上比例不超过
等级为不合格,原则上比例不超过![]() .该省某校高二年级学生都参加学业水平考试,先从中随机抽取了部分学生的考试成绩进行统计,统计结果如图所示.若该校高二年级共有1000名学生,则估计该年级拿到
.该省某校高二年级学生都参加学业水平考试,先从中随机抽取了部分学生的考试成绩进行统计,统计结果如图所示.若该校高二年级共有1000名学生,则估计该年级拿到![]() 级及以上级别的学生人数有( )
级及以上级别的学生人数有( )
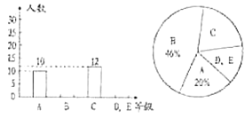
A.45人B.660人C.880人D.900人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的极值;
的极值;
(2)问:是否存在实数![]() ,使得
,使得![]() 有两个相异零点?若存在,求出
有两个相异零点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com