
【题目】已知函数f(x)=lnx﹣ax2(a∈R)
(Ⅰ) 讨论f(x)的单调性;
(Ⅱ) 若对于x∈(0,+∞),f(x)≤a﹣1恒成立,求实数a的取值范围.
【答案】解:(Ⅰ)函数f(x)的定义域为(0,+∞). 因为 ![]() ,
,
所以:(i)当a≤0时,f'(x)>0对x∈(0,+∞)恒成立,
所以f(x)在(0,+∞)上单调递增;
(ii)当a>0时,令 ![]() 或
或 ![]() (舍)
(舍)
当 ![]() 时,f'(x)>0;当
时,f'(x)>0;当 ![]() 时,f'(x)<0.
时,f'(x)<0.
所以f(x)在 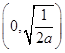 上单调递增;f(x)在
上单调递增;f(x)在  上单调递减.
上单调递减.
(Ⅱ)令g(x)=f(x)﹣a+1=lnx﹣ax2﹣a+1(x>0)
则依题意,g(x)=lnx﹣ax2﹣a+1≤0对x∈(0,+∞)恒成立.
由于 ![]() ,所以由(1)可知:
,所以由(1)可知:
当a≤0时,g(x)在(0,+∞)上单调递增;
当a>0时,g(x)在 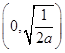 上单调递增;在
上单调递增;在  上单调递减.
上单调递减.
此时,g(x)在 ![]() 处取得最大值.
处取得最大值.
若a≤0,因为g(1)=﹣2a+1>0,显然与题设相矛盾;
若a>0,则题设等价于 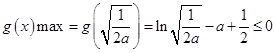 (*),
(*),
不妨设 ![]() ,则
,则 ![]() .
.
所以(*)式等价转化为 ![]() (t>0).
(t>0).
记 ![]() ,则F(1)=0.
,则F(1)=0.
因为 ![]() ,所以F(t)在(0,+∞)上单调递增.
,所以F(t)在(0,+∞)上单调递增.
所以F(t)≤00<t≤1,
即: ![]() ,解得,
,解得, ![]() .
.
所以所求的实数a的取值范围为 ![]()
【解析】(Ⅰ)求出函数的导数,通过讨论a的范围求出函数的单调区间即可;(Ⅱ)根据g(x)=lnx﹣ax2﹣a+1≤0对x∈(0,+∞)恒成立.求出函数的导数,通过讨论a的范围,判断函数的单调性,从而求出a的范围即可.
【考点精析】关于本题考查的利用导数研究函数的单调性,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点与双曲线
的焦点与双曲线![]() 的焦点重合,并且经过点
的焦点重合,并且经过点![]() .
.
(Ⅰ)求椭圆C的标准方程;
(II) 设椭圆C短轴的上顶点为P,直线![]() 不经过P点且与
不经过P点且与![]() 相交于
相交于![]() 、
、![]() 两点,若直线PA与直线PB的斜率的和为
两点,若直线PA与直线PB的斜率的和为![]() ,判断直线
,判断直线![]() 是否过定点,若是,求出这个定点,否则说明理由.
是否过定点,若是,求出这个定点,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的各项均为正数,其前n项和为Sn , 已知 ![]()
![]() =1,且a1=
=1,且a1= ![]() ,则tanSn的取值集合是( )
,则tanSn的取值集合是( )
A.{0, ![]() }
}
B.{0, ![]() ,
, ![]() }
}
C.{0, ![]() ,﹣
,﹣ ![]() }
}
D.{0, ![]() ,﹣
,﹣ ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣4|,g(x)=a|x|,a∈R.
(Ⅰ)当a=2时,解关于x的不等式f(x)>2g(x)+1;
(Ⅱ)若不等式f(x)≥g(x)﹣4对任意x∈R恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义区间[x1 , x2]的长度为x2﹣x1(x2>x1)单调递增),函数 ![]() (a∈R,a≠0)的定义域与值域都是[m,n](n>m),则区间[m,n]取最大长度时实数a的值( )
(a∈R,a≠0)的定义域与值域都是[m,n](n>m),则区间[m,n]取最大长度时实数a的值( )
A.![]()
B.﹣3
C.1
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为 . (参考数据:sin15°=0.2588,sin7.5°=0.1305) 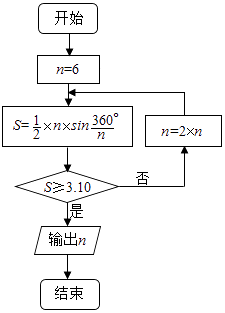
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com