【题目】一个口袋中装有9个大小形状完全相同的球，球的编号分别为1，2，…，9，随机摸出两个球，则两个球的编号之和大于9的概率是______（结果用分数表示）.
【答案】
【解析】
由题意分别列举两个球编号之和大于9的号码，再用古典概型公式求概率．
解：当抽出的其中一个球为1号时，另一个球的号码为9，
当抽出的其中一个球为2号时，另一个球的号码为9，8，
当抽出的其中一个球为3号时，另一个球的号码为9，8，7，
当抽出的其中一个球为4号时，另一个球的号码为9，8，7，6，
当抽出的其中一个球为5号时，另一个球的号码为9，8，7，6，
当抽出的其中一个球为6号时，另一个球的号码为9，8，7，
当抽出的其中一个球为7号时，另一个球的号码为9，8，
当抽出的其中一个球为8号时，另一个球的号码为9，
所以两个球编号之和大于9的情况有1＋2＋3＋4＋4＋3＋2＋1＝20种，
总的抽取情况有
种，所以两个球编号之和大于9的概率是
，
故答案为：．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知抛物线
：
的焦点为
，抛物线上存在一点
到焦点的距离等于3.
（1）求抛物线的方程；
（2）过点的直线
交抛物线于
，
两点，以线段
为直径的圆交
轴于
，
两点，设线段的中点为
，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左右焦点分别为
，离心率为
；圆
过椭圆
的三个顶点.过点
且斜率不为0的直线
与椭圆交于
两点.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）证明：在
轴上存在定点
，使得
为定值；并求出该定点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《九章算术》中，将底面为长方形且有一条侧棱与地面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑，首届中国国际进口博览会的某展馆棚顶一角的钢结构可以抽象为空间图形阳马，如图所示，在阳马
中，
底面
.
（1）已知
，斜梁
与底面所成角为
，求立柱
的长；（精确到
）
（2）求证：四面体
为鳖臑.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（其中
，
，
，
是实数常数，
）.
（1）若
，函数
的图象关于点
成中心对称，求，的值；
（2）若函数满足条件（1），且对任意
，总有
，求的取值范围；
（3）若
，函数是奇函数，
，
，且对任意
时，不等式
恒成立，求负实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】十七世纪，法国数学家费马提出猜想；“当整数
时，关于
、
、
的方程
没有正整数解”，经历三百多年，1995年英国数学家安德鲁
怀尔斯给出了证明，使它终成费马大定理，则下面命题正确的是（ ）
①对任意正整数
，关于、、的方程都没有正整数解；
②当整数时，关于、、的方程至少存在一组正整数解；
③当正整数
时，关于、、的方程至少存在一组正整数解；
④若关于、、的方程至少存在一组正整数解，则正整数；
A.①②/span>B.①③C.②④D.③④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】无穷数列
、
、
满足：
，
，
，
，记
（
表示3个实数
、
、
中的最大数）.
（1）若
，
，
，求数列
的前
项和
；
（2）若
，
，
，当
时，求满足条件
的
的取值范围；
（3）证明：对于任意正整数
、
、
，必存在正整数
，使得
，
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的左右焦点为
，
，
是椭圆上半部分的动点，连接和长轴的左右两个端点所得两直线交
正半轴于
，
两点（点在的上方或重合）.
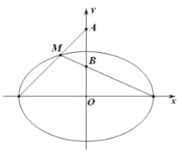
（1）当
面积
最大时，求椭圆的方程；
（2）当
时，若是线段
的中点，求直线
的方程；
（3）当
时，在
轴上是否存在点
使得
为定值，若存在，求点的坐标，若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某种商品原来毎件售价为25元,年销售8万件.
(1)据市场调查，若价格毎提高1元，销售量将相应瑊少2000件,要使销售的总收入不低于原收入，该商品每件定价最多为多少？
(2)为了扩大商品的影响力,提高年销售量，公司决定明年对该商品进行全面技术革新和营销策略改革,并提高价格到
元,公司拟投入
万元作为技改费用,投入50万元作为固定宣传费用，试问:该商品明年的销售量
至少达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时每件商品的定价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com