
【题目】海关对同时从![]() 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如表所示,工作人员用分层抽样的方法从这些商品中共抽取7件样品进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如表所示,工作人员用分层抽样的方法从这些商品中共抽取7件样品进行检测.
地区 |
|
|
|
数量 | 200 | 50 | 100 |
(1)求这7件样品中来自![]() 各地区样品的数量;
各地区样品的数量;
(2)若在这7件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
【答案】(1)4,1,2;(2)![]() .
.
【解析】
(1)先计算出抽样比,进而可求出这7件样品来自![]() ,
,![]() ,
,![]() 各地区商品的数量;
各地区商品的数量;
(2)先计算在这7件样品中随机抽取2件的基本事件总数,及这2件商品来自相同地区的事件个数,代入古典概型概率计算公式,可得答案;
解:(1)∵样本容量与总体中的个数的比为![]()
∴样本中包含三个地区的个体数量分别为:
![]() ,
,![]() ,
,![]()
∴![]() 三个地区的商品被选取的件数分别为4,1,2.
三个地区的商品被选取的件数分别为4,1,2.
(2)设7件来自![]() 三个地区的样品分别为:
三个地区的样品分别为:![]()
解从7件样品中抽取的这2件商品构成的所有基本事件为:
![]()
![]()
![]() ,共21个.
,共21个.
每个样品被抽到的机会均等,因此这些基本事件的出现是等可能的.
记事件![]() :“抽取的这2件商品来自相同地区,”,则事件
:“抽取的这2件商品来自相同地区,”,则事件![]() 包含的基本事件有:
包含的基本事件有:
![]() 共7个.
共7个.
所以![]() ,即这2件商品来自相同地区的概率为
,即这2件商品来自相同地区的概率为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且过点
的焦点重合,且过点![]() .过点
.过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 为椭圆的左顶点.
为椭圆的左顶点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)求![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市公交公司为了鼓励广大市民绿色出行,计划在某个地段增设一个起点站,为了研究车辆发车的间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过抽样调查五个不同时段的情形,统计得到如下数据:
之间的关系,经过抽样调查五个不同时段的情形,统计得到如下数据:
间隔时间( | 8 | 10 | 12 | 14 | 16 |
等候人数( | 16 | 19 | 23 | 26 | 29 |
调查小组先从这5组数据中选取其中的4组数据求得线性回归方程,再用剩下的1组数据进行检验,检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过1,则称所求的回归方程是“理想回归方程”.
的差,若差值的绝对值不超过1,则称所求的回归方程是“理想回归方程”.
(1)若选取的是前4组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断所求方程是否是“理想回归方程”;
,并判断所求方程是否是“理想回归方程”;
(2)为了使等候的乘客不超过38人,试用所求方程估计间隔时间最多可以设为多少分钟?
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)设![]() ,求证:数列{bn}是等差数列,并求出{an}的通项公式.
,求证:数列{bn}是等差数列,并求出{an}的通项公式.
(2)设![]() ,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得
,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得![]() 对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二期中考试后,教务处计划对全年级数学成绩进行统计分析,从男、女生中各随机抽取100名学生,分别制成了男生和女生数学成绩的频率分布直方图,如图所示.

(1)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(2)在(1)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有1名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 与曲线
与曲线![]() 的直角坐标方程:
的直角坐标方程:
(Ⅱ)过点![]() 平行于直线
平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 轨迹的直角坐标方程.
轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“纪念抗日战争胜利73周年”的知识竞赛,从参加竞赛的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() ,…,
,…,![]() 后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:
后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:
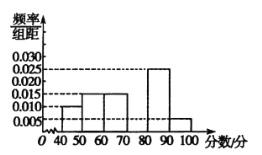
(1)求第四组的频率,并补全这个频率分布直方图;
(2)估计这次竞赛的及格率(60分及以上为及格)和平均分(同一组中的数据用该组区间的中点值代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时, ![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,并根据图象:
轴左侧的图象,如图所示,并根据图象:

(1)直接写出函数![]() ,
, ![]() 的增区间;
的增区间;
(2)写出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com