
【题目】已知正方形的中心为![]() ,一边所在直线的方程为
,一边所在直线的方程为![]() ,求其他三边所在的直线方程.
,求其他三边所在的直线方程.
【答案】![]() .
.
【解析】试题分析:先求出正方形中心![]() 到直线
到直线![]() 的距离,然后根据两直线平行、两直线垂直斜率之间的关系,求出未知直线的斜率,设出所求直线方程,利用正方形的中心到三边等距离,分别求出所设直线方程中的斜率,从而可得到其他三边所在的直线方程.
的距离,然后根据两直线平行、两直线垂直斜率之间的关系,求出未知直线的斜率,设出所求直线方程,利用正方形的中心到三边等距离,分别求出所设直线方程中的斜率,从而可得到其他三边所在的直线方程.
试题解析:正方形中心G(-1,0)到四边距离均为![]() ,
,
设正方形与已知直线平行的一边所在直线方程为x+3y+C1=0,
则![]() ,
,
即|C1-1|=6.
解得C1=-5(舍去)或C1=7.
故与已知边平行的直线方程为
x+3y+7=0.
设正方形另一组对边所在直线方程为
3x-y+C2=0,
则![]()
即|C2-3|=6.
解得C2=9或C2=-3.
所以正方形另两边所在直线的方程为
3x-y+9=0和3x-y-3=0.
综上所述,正方形其他三边所在直线的方程分别为:
x+3y+7=0,3x-y+9=0,3x-y-3=0.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
【题目】下面四个关于圆锥曲线的命题中,其中真命题为( )
A.设A、B为两个定点,K为非零常数,若![]() ,则动点P的轨迹是双曲线
,则动点P的轨迹是双曲线
B.方程![]() 的两根可分别作为椭圆和双曲线的离心率
的两根可分别作为椭圆和双曲线的离心率
C.双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点
有相同的焦点
D.已知抛物线![]() ,以过焦点的一条弦AB为直径作圆,则此圆与准线相切
,以过焦点的一条弦AB为直径作圆,则此圆与准线相切
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区为了了解本年度数学竞赛成绩情况,从中随机抽取了![]() 个学生的分数作为样本进行统计,按照
个学生的分数作为样本进行统计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图所示,已知得分在
的分组作出频率分布直方图如图所示,已知得分在![]() 的频数为20,且分数在70分及以上的频数为27.
的频数为20,且分数在70分及以上的频数为27.
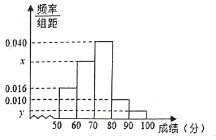
(1)求样本容量![]() 以及
以及![]() ,
,![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接“五一”节的到来,某单位举行“庆五一,展风采”的活动.现有6人参加其中的一个节目,该节目由![]() 两个环节可供参加者选择,为增加趣味性,该单位用电脑制作了一个选择方案:按下电脑键盘“Enter”键则会出现模拟抛两枚质地均匀骰子的画面,若干秒后在屏幕上出现两个点数
两个环节可供参加者选择,为增加趣味性,该单位用电脑制作了一个选择方案:按下电脑键盘“Enter”键则会出现模拟抛两枚质地均匀骰子的画面,若干秒后在屏幕上出现两个点数![]() 和
和![]() ,并在屏幕的下方计算出
,并在屏幕的下方计算出![]() 的值.现规定:每个人去按“Enter”键,当显示出来的
的值.现规定:每个人去按“Enter”键,当显示出来的![]() 小于
小于![]() 时则参加
时则参加![]() 环节,否则参加
环节,否则参加![]() 环节.
环节.
(1)求这6人中恰有2人参加该节目![]() 环节的概率;
环节的概率;
(2)用![]() 分别表示这6个人中去参加该节目
分别表示这6个人中去参加该节目![]() 两个环节的人数,记
两个环节的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为奇函数,
为奇函数,![]() 为偶函数,且
为偶函数,且![]() .
.
(1)求![]() 及
及![]() 的解析式及定义域;
的解析式及定义域;
(2)如函数![]() 在区间
在区间![]() 上为单调函数,求实数
上为单调函数,求实数![]() 的范围.
的范围.
(3)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=![]() x上时,求直线AB的方程.
x上时,求直线AB的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 设椭圆![]() 的左焦点为
的左焦点为![]() ,左顶点为
,左顶点为![]() ,顶点为B.已知
,顶点为B.已知![]() (
(![]() 为原点).
为原点).
(Ⅰ)求椭圆的离心率;
(Ⅱ)设经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆在
与椭圆在![]() 轴上方的交点为
轴上方的交点为![]() ,圆
,圆![]() 同时与
同时与![]() 轴和直线
轴和直线![]() 相切,圆心
相切,圆心![]() 在直线
在直线![]() 上,且
上,且![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
(1)证明|EA|+|EB|为定值,并写出点E的轨迹方程;
(2)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com