【题目】已知函数f（x）=3x+x，g（x）=x3+x，h（x）=log3x+x的零点依次为a，b，c，则（ ）
A.c＜b＜a
B.a＜b＜c
C.c＜a＜b
D.b＜a＜c
【答案】B
【解析】解：（1）令f（x）=3x+x=0，即3x+x=0，化为3x=x，分别作出函数y=3x ， y=﹣x的图象 由图象可以知道函数f（x）的零点a＜0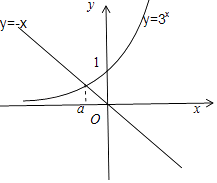
2）对于函数对于函数g（x）=x3+x=x（x2+1），令h（x）=0，则x=0，
∴b=0；
3）令h（x）=log3x+x=0，则log3x+x=0，即log3x=﹣x，分别作出函数y=log3x，y=﹣x的图象，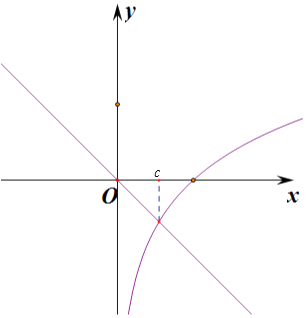
则c＞0，
综上可知：a＜b＜c，
故选B．
由3x+x=0，化为3x=x，分别作出函数y=3x ， y=﹣x的图象由图象可以知道函数f（x）的零点a＜0，令h（x）=0，则x=0，b=0，由h（x）=0，即log3x=﹣x，分别作出函数y=log3x，y=﹣x的图象，即可求得
a，b和c的大小关系．
一线名师权威作业本系列答案科目：高中数学 来源： 题型：
【题目】已知函数
.
（Ⅰ）若曲线
在点
处的切线与直线
垂直，求实数
的值；
（Ⅱ）若函数
在其定义域上是增函数，求实数
的取值范围；
（Ⅲ）当
时，函数
的两个极值点为
，且
，若不等式
恒成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=2sin2x+2 
sinxsin（x+ 
）（ω＞0）．
（1）求f（x）的最小正周期；
（2）求函数f（x）在区间[0， 
]上的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设△ABC是边长为1的正三角形，点P1 ， P2 ， P3四等分线段BC（如图所示）．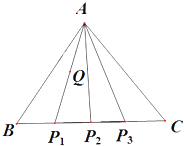
（1）求 
+ 
的值；
（2）Q为线段AP1上一点，若 
=m + 
，求实数m的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“斐波那契数列”是数学史上一个著名数列，在斐波那契数列{an}中，a1=1，a2=1，an+2=an+1+an（n∈N*）则a8=；若a2018=m2+1，则数列{an}的前2016项和是 ． （用m表示）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商场在店庆一周年开展“购物折上折活动”：商场内所有商品按标价的八折出售，折后价格每满500元再减100元．如某商品标价为1500元，则购买该商品的实际付款额为1500×0.8-200=1000（元）．设购买某商品得到的实际折扣率
．设某商品标价为
元，购买该商品得到的实际折扣率为
．
（Ⅰ）写出当
时， 
关于
的函数解析式，并求出购买标价为1000元商品得到的实际折扣率；
（Ⅱ）对于标价在［2500,3500］的商品，顾客购买标价为多少元的商品，可得到的实际折扣率低于
？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=3x2+2（k﹣1）x+k+5．
（1）求函数f（x）在[0，3]上最大值；
（2）若函数f（x）在[0，3]上有零点，求实数k的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
