
【题目】设集合A=R,集合B={y|y>0},下列对应关系中是从集合A到集合B的映射的是( )
A.x→y=|x|
B.x→y= ![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵|0|=0,而 0R+ , 集合A中的元素0在集合B中没有像,故选项A 不是映射.
对于选项B,集合A中的元素1在集合B中没有像,故选项B不是映射.
对于选项C,集合A中的所有元素在集合B中都有唯一的像和它对应,故选项C是映射.
对于选项D,由于函数的定义域不是R,故选项D不是映射.
故选 C.
【考点精析】掌握映射的相关定义是解答本题的根本,需要知道对于映射f:A→B来说,则应满足:(1)集合A中的每一个元素,在集合B中都有象,并且象是唯一的;(2)集合A中不同的元素,在集合B中对应的象可以是同一个;(3)不要求集合B中的每一个元素在集合A中都有原象;注意:映射是针对自然界中的所有事物而言的,而函数仅仅是针对数字来说的.所以函数是映射,而映射不一定的函数.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an=3an﹣1+3n﹣1(n∈N*,n≥2)且a3=95.
(1)求a1 , a2的值;
(2)求实数t,使得bn= ![]() (an+t)(n∈N*)且{bn}为等差数列;
(an+t)(n∈N*)且{bn}为等差数列;
(3)在(2)条件下求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣log3(9x)log3 ![]() (
( ![]() ≤x≤27).
≤x≤27).
(1)设t=log3x,求t的取值范围
(2)求f(x)的最小值,并指出f(x)取得最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程x2+mx+1=0有两个不等的负实数根;命题q:方程4x2+4(m﹣2)x+1=0无实数根.
(1)若“¬p”为假命题,求m范围;
(2)若“p或q”为真命题,“p且q”为假命题,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某公路![]() 一侧有一块空地
一侧有一块空地![]() ,其中
,其中 ![]() ,
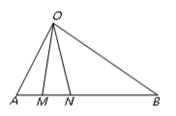
,![]() .当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
.当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
(1)若M在距离A点2 km处,求点M,N之间的距离;
(2)为节省投入资金,人工湖△OMN的面积要尽可能小.试确定M的位置,使△OMN的面积最小,并求出最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若{ ![]() 、
、 ![]() 、
、 ![]() }为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
}为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
A.![]() ,
, ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
B.![]() ,
, ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
C.![]() ,
, ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
D.![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]() ,
, ![]() +2
+2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数g(x)=f(x)+2x,x∈R为奇函数.
(1)判断函数f(x)的奇偶性;
(2)若x>0时,f(x)=log3x,求函数g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示. 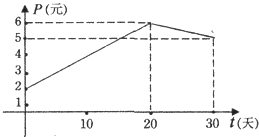
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI 是居民消费价格指数(consumer price index)的简称.居民消费价格指数,是一个反映居民家庭一般所购买的消费品价格水平变动情况的宏观经济指标.下面是根据统计局发布的2017年1月一7月的CPI 同比增长与环比增长涨跌幅数据绘制的折线图.(注:2017 年2月与2016年2月相比较,叫同比;2017 年2 月与2017 年1月相比较,叫环比)根据该折线图,则下列结论错误的是( )
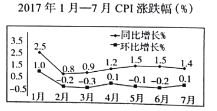
A. 2017 年1月一7月分别与2016年1月一7月相比较,CPI 有涨有跌
B. 2017 年1月一7月CPI 有涨有跌
C. 2017年1月一7月分别与2016年1月一7月相比较,1月CPI 涨幅最大
D. 2017 年2 月一7月CPI 涨跌波动不大,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com