Question

【题目】给出下列命题：

①若 ， 是第一象限角且 ，则 ；

②函数 在上是减函数；

③ 是函数 的一条对称轴；

④函数 的图象关于点 成中心对称；

⑤设 ，则函数 的最小值是，其中正确命题的序号为 __________．

Answer 1

【答案】③⑤

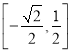【解析】对于①，时， ，而，故①错误；对于②，在上递增，故②错误；对于③，时， ， 是的对称轴，故③正确；对于④，时， 不是的对称中心，故④错误；对于⑤，，设因为 ，所以,则 ， 在上递增，在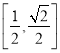 上递减，因为 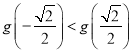可得时， ，即函数 的最小值是，故⑤正确，故答案为③⑤.

【 方法点睛】本题主要通过对多个命题真假的判断，综合考查三角函数的单调性、三角函数的奇偶性、三角函数的图象与性质，属于难题.这种题型综合性较强，也是高考的命题热点，同学们往往因为某一处知识点掌握不好而导致“全盘皆输”，因此做这类题目更要细心、多读题，尽量挖掘出题目中的隐含条件，另外，要注意从简单的自己已经掌握的知识点入手，然后集中精力突破较难的命题.