
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.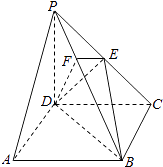
(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C﹣PB﹣D的大小.
【答案】
(1)解:方法一:证明:连接AC,AC交BD于O,连接EO.
∵底面ABCD是正方形,∴点O是AC的中点
在△PAC中,EO是中位线,∴PA∥EO
而EO平面EDB且PA平面EDB,
所以,PA∥平面EDB
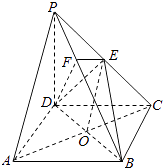
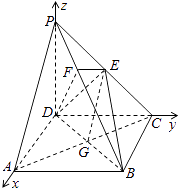
方法二:如图所示建立空间直角坐标系,D为坐标原点,设DC=a.
证明:连接AC,AC交BD于G,连接EG.
依题意得 ![]() .
.
∵底面ABCD是正方形,∴G是此正方形的中心,故点G的坐标为 ![]() 且
且 ![]() .
.
∴ ![]() ,这表明PA∥EG.
,这表明PA∥EG.
而EG平面EDB且PA平面EDB,∴PA∥平面EDB
(2)解:方法一,证明:
∵PD⊥底面ABCD且DC底面ABCD,∴PD⊥DC
∵PD=DC,可知△PDC是等腰直角三角形,而DE是斜边PC的中线,
∴DE⊥PC.①
同样由PD⊥底面ABCD,得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC.
而DE平面PDC,∴BC⊥DE.②
由①和②推得DE⊥平面PBC.
而PB平面PBC,∴DE⊥PB
又EF⊥PB且DE∩EF=E,所以PB⊥平面EFD
方法二:证明;依题意得B(a,a,0), ![]() .
.
又 ![]() ,故
,故 ![]() .
.
∴PB⊥DE.
由已知EF⊥PB,且EF∩DE=E,所以PB⊥平面EFD
(3)解:方法一:由(2)知,PB⊥DF,故∠EFD是二面角C﹣PB﹣D的平面角.
由(2)知,DE⊥EF,PD⊥DB.
设正方形ABCD的边长为a,
则 ![]()
![]() ,
, ![]()
![]() .
.
在Rt△PDB中, ![]() .
.
在Rt△EFD中, 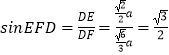 ,∴
,∴ ![]() .
.
所以,二面角C﹣PB﹣D的大小为 ![]()
方法二:解:设点F的坐标为(x0,y0,z0), ![]() ,则(x0,y0,z0﹣a)=λ(a,a,﹣a).
,则(x0,y0,z0﹣a)=λ(a,a,﹣a).
从而x0=λa,y0=λa,z0=(1﹣λ)a.所以 ![]() .
.
由条件EF⊥PB知, ![]() ,即
,即 ![]() ,解得
,解得 ![]()
∴点F的坐标为 ![]() ,且
,且 ![]() ,
, ![]()
∴ ![]()
即PB⊥FD,故∠EFD是二面角C﹣PB﹣D的平面角.
∵ ![]() ,且
,且 ![]() ,
, ![]() ,
,
∴ 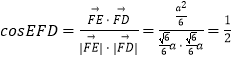 .
.
∴ ![]() .
.
所以,二面角C﹣PB﹣D的大小为 ![]() .
.
【解析】法一:(1)连接AC,AC交BD于O,连接EO要证明PA∥平面EDB,只需证明直线PA平行平面EDB内的直线EO;(2)要证明PB⊥平面EFD,只需证明PB垂直平面EFD内的两条相交直线DE、EF,即可;(3)必须说明∠EFD是二面角C﹣PB﹣D的平面角,然后求二面角C﹣PB﹣D的大小.法二:如图所示建立空间直角坐标系,D为坐标原点,设DC=a.(1)连接AC,AC交BD于G,连接EG,求出 ![]() ,即可证明PA∥平面EDB;(2)证明EF⊥PB,
,即可证明PA∥平面EDB;(2)证明EF⊥PB, ![]() ,即可证明PB⊥平面EFD;(3)求出
,即可证明PB⊥平面EFD;(3)求出 ![]() ,利用
,利用 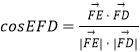 ,求二面角C﹣PB﹣D的大小.
,求二面角C﹣PB﹣D的大小.


科目:高中数学 来源: 题型:
【题目】2017年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如下表:
评估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
评分类型 | D | C | B | A |
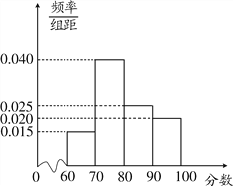 考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
(Ⅰ)评分类型为A的商业连锁店有多少家;
(Ⅱ)现从评分类型为A,D的所有商业连锁店中随机抽取两家做分析,求这两家来自同一评分类型的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从参加环保知识竞赛的学生中抽出40名,将其成绩(均为整数)整理后画出的频率分布直方图如下:

观察图形,回答下列问题:
(1)估计这次环保知识竞赛成绩的中位数;
(2)从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:
①乘积(a+b+c+d)(p+q+r)(m+n)展开式的项数是24;
②由1、2、3、4、5组成没有重复数字且1、2都不与5相邻的五位数的个数是36;
③某会议室第一排共有8个座位,现有3人就座,若要求每人左右均有空位,那么不同的坐法种数为24;
④已知(1+x)8=a0+a1x+…+a8x8 , 其中a0 , a1 , …,a8中奇数的个数为2.
其中真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定两个长度为1的平面向量 ![]() 和
和 ![]() ,它们的夹角为120°.如图所示,点C在以O为圆心的圆弧
,它们的夹角为120°.如图所示,点C在以O为圆心的圆弧 ![]() 上变动.若
上变动.若 ![]() ,其中x,y∈R,试求x+y的最大值.
,其中x,y∈R,试求x+y的最大值. 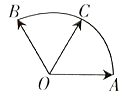
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为预防H1N1病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如表:
A组 | B组 | C组 | |
疫苗有效 | 673 | x | y |
疫苗无效 | 77 | 90 | z |
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求x的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知y≥465,z≥25,求不能通过测试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)(ω>0,||< ![]() ,x∈R)的部分图象如图所示,则函数表达式为( )
,x∈R)的部分图象如图所示,则函数表达式为( ) 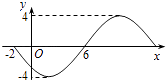
A.y=﹣4sin( ![]() )
)
B.y=4sin( ![]() )
)
C.y=﹣4sin( ![]() )
)
D.y=4sin( ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com