
| A. | 20$\sqrt{2}$ | B. | 20 | C. | 20$\sqrt{3}$ | D. | 10$\sqrt{2}$ |
分析 由题意画出图形:∠A=45°,∠ACB=105°,推出∠B,求出AC,利用三角形求出CD,然后求BC.
解答 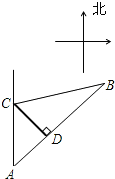 解:由题意画出图形,如图过C作CD⊥AB于D,
解:由题意画出图形,如图过C作CD⊥AB于D,
在Rt△ACD中,AC=20×1=20,∠A=45°,
∴sinA=$\frac{CD}{AC}$.
∴CD=AC•sinA=20×$\frac{\sqrt{2}}{2}$=10$\sqrt{2}$.
在Rt△BCD中,∠B=∠PCB-∠A=75°-45°=30°,
∴BC=2•CD=2×10$\sqrt{2}$=20$\sqrt{2}$(n mile).
∴此时船与灯塔的距离BC为20$\sqrt{2}$n mile.
故选:A.
点评 本题考查三角形的实际应用,转化思想的应用,考查计算能力,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,2] | C. | [2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
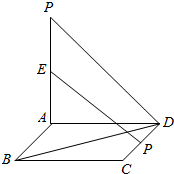 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间t/天 | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量 m/件 | 94 | 90 | 84 | 76 | 24 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
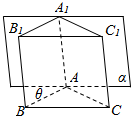 已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )
已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )| A. | $\sqrt{3}$ | B. | 4 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com