练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设P是△ABC内一点，△ABC三边上的高分别为hA、hB、hC，P到三边的距离依次为la、lb、lc，则有
    la
    hA
    +
    lb
    hB
    +
    lc
    hC
    =1；类比到空间，设P是四面体ABCD内一点，四顶点到对面的距离分别是hA、hB、hC、hD，P到这四个面的距离依次是la、lb、lc、ld，则有
    la
    hA
    +
    lb
    hB
    +
    lc
    hC
    +
    ld
    hD
    =1
    la
    hA
    +
    lb
    hB
    +
    lc
    hC
    +
    ld
    hD
    =1
    ．
    分析：在平面中利用面积分割法，结合三角形面积公式证出
    la
    hA
    +
    lb
    hB
    +
    lc
    hC
    =1，结论成立．依此可得当P为四面体ABCD内一点时，利用体积分割法和锥体的体积公式，类似于平面中结论的证明方法可得
    la
    hA
    +
    lb
    hB
    +
    lc
    hC
    +
    ld
    hD
    =1，得到本题答案．
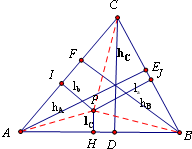    解答：解：如图，连结PA、PB、PC，可得
    S△ABP+S△BCP+S△CAP=S△ABC，
    即
    1
    2
    AB×lc+
    1
    2
    BC×la+
    1
    2
    CA×lb=S△ABC，…（1）
    ∵S△ABC=
    1
    2
    AB×hC=
    1
    2
    BC×hA=
    1
    2
    CA×hB
    ∴在（1）式的两边都除以S△ABC，得
    lc
    h C
    +
    la
    h A
    +
    lb
    h B
    =1
    即
    la
    hA
    +
    lb
    hB
    +
    lc
    hC
    =1，即平面内的结论成立
    当P为四面体ABCD内一点时，VP-BCD+VP-CDA+VP-ABD+VP-ABC=VD-ABC，
    两边都除以VD-ABC，得
    VP-BCD
    VD-ABC
    +
    VP-CDA
    VD-ABC
    +
    VP-ABD
    VD-ABC
    +
    VP-ABC
    VD-ABC
    =1
    类似平面中结论证明的方法，可得
    la
    hA
    +
    lb
    hB
    +
    lc
    hC
    +
    ld
    hD
    =1
    故答案为：
    la
    hA
    +
    lb
    hB
    +
    lc
    hC
    +
    ld
    hD
    =1
    点评：本题给出三角形ABC内一点P满足的等式，要求给出空间四面体的一个类似结论．着重考查了三角形面积公式、锥体的体积公式和类比推理的一般方法等知识，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：新课标高三数学推理与证明专项训练（河北） 题型：填空题

    设P是△ABC内一点，△ABC三边上的高分别为hA、hB、hC，P到三边的距离依次为la、lb、lc，则有＋＋＝______；类比到空间，设P是四面体ABCD内一点，四顶点到对面的距离分别是hA、hB、hC、hD，P到这四个面的距离依次是la、lb、lc、ld，则有________

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设P是△ABC内一点，三个顶点到对边的距离分别为hA,hB,hC，P到对应三边的距离依次为lA,lB,lC,则有=______________；类比到空间，设P为四面体ABCD内一点，四个顶点到对面的距离分别是hA,hB,hC,hD，P到这四个面的距离依次是lA,lB,lC,lD，则有______________.

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广东省揭阳一中高二（下）第一次段考数学试卷（理科）（解析版） 题型：填空题

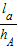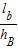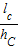    设P是△ABC内一点，△ABC三边上的高分别为hA、hB、hC，P到三边的距离依次为la、lb、lc，则有++=1；类比到空间，设P是四面体ABCD内一点，四顶点到对面的距离分别是hA、hB、hC、hD，P到这四个面的距离依次是la、lb、lc、ld，则有    ．

    查看答案和解析>>

    科目：高中数学 来源：0108 模拟题 题型：填空题

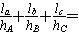    设P是△ABC内一点，三个顶点到对边的距离分别为hA、hB、hC，P到对应三边的距离依次为la、lb、lc，则有（    ）；类比到空间，设P为四面体ABCD内一点，四个顶点到对面的距离分别是hA、hB、hC、hD，P 到这四个面的距离依次是la、lb、lc、ld，则有（    ）。

    查看答案和解析>>

    同步练习册答案