
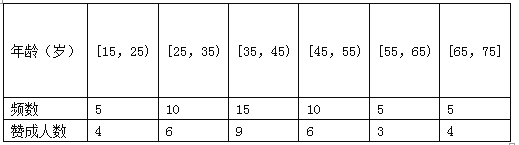
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(Ⅰ)完成被调查人员的频率分布直方图;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)图见解析
(2)![]()
(3)所以![]() 的分布列是:
的分布列是:
|
|
|
|
|
|
|
|
|
|
![]() 的数学期望
的数学期望![]() .
.
【解析】试题分析:(1)由已知求出各组的频率和纵坐标,由此作出被调查人员的频率分布直方图。
(2)由表知年龄在![]() 内的有5人,不赞成的有1人,年龄在
内的有5人,不赞成的有1人,年龄在![]() 内的有10人,不赞成的有4人,由此利用互斥事件概率计算公式能求出恰有2人不赞成的概率;
内的有10人,不赞成的有4人,由此利用互斥事件概率计算公式能求出恰有2人不赞成的概率;
(3)![]() 的所有可能取值为
的所有可能取值为![]() ,分别求出相应的概率,由此能求出随机变量
,分别求出相应的概率,由此能求出随机变量![]() 的分布列和数学期望。
的分布列和数学期望。
试题解析::(Ⅰ)各组的频率分别为0.1,0.2,0.3,0.2,0.1,0.1,所以图中各组的纵坐标分别,0.01,0.02,0.03,0.02,0.01,0.01

(Ⅱ)由表知,年龄在![]() 内有5人,不赞成的有1人,年龄在
内有5人,不赞成的有1人,年龄在![]() 内有10人,不赞成的有4人,恰有两人不赞成的概率为
内有10人,不赞成的有4人,恰有两人不赞成的概率为
![]()
(Ⅲ)由已知得,![]() 的所有取值为0,1,2,3.
的所有取值为0,1,2,3.
![]()
![]()
![]()
所以![]() 的分布列是:
的分布列是:

所以![]() 的数学期望
的数学期望![]()


科目:高中数学 来源: 题型:
【题目】下列结论正确的个数是( )
①命题“所有的四边形都是矩形”是特称命题;
②命题“x∈R,x2+2<0”是全称命题;
③若p:x∈R,x2+4x+4≤0,则q:x∈R,x2+4x+4≤0是全称命题.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)既是奇函数,又是周期为3的周期函数,当x∈(0, ![]() )时,f(x)=sinπx,f(
)时,f(x)=sinπx,f( ![]() )=0,则函数f(x)在区间[0,6]上的零点个数是( )
)=0,则函数f(x)在区间[0,6]上的零点个数是( )
A.9
B.7
C.5
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:f(x)= ![]() 在区间(1,+∞)上是减函数;命题q;x1x2是方程x2﹣ax﹣2=0的两个实根,不等式m2+5m﹣3≥|x1﹣x2|对任意实数α∈[﹣1,1]恒成立;若¬p∧q为真,试求实数m的取值范围.
在区间(1,+∞)上是减函数;命题q;x1x2是方程x2﹣ax﹣2=0的两个实根,不等式m2+5m﹣3≥|x1﹣x2|对任意实数α∈[﹣1,1]恒成立;若¬p∧q为真,试求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为非负整数的数列![]() 同时满足下列条件:
同时满足下列条件:
①![]()
![]() ;②
;②![]()
![]() ;③
;③![]() 是
是![]() 的因数(
的因数(![]() ).
).
(Ⅰ)当![]() 时,写出数列
时,写出数列![]() 的前五项;
的前五项;
(Ⅱ)若数列![]() 的前三项互不相等,且
的前三项互不相等,且![]() 时,
时, ![]() 为常数,求
为常数,求![]() 的值;
的值;
(Ⅲ)求证:对任意正整数![]() ,存在正整数
,存在正整数![]() ,使得
,使得![]() 时,
时, ![]() 为常数.
为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线C的中心在原点,右焦点为 ![]() ,渐近线方程为
,渐近线方程为 ![]() .
.
(1)求双曲线C的方程;
(2)设直线l:y=kx+1与双曲线C交于A、B两点,问:当k为何值时,以AB为直径的圆过原点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E. 
(1)若D为AC的中点,证明:DE是⊙O的切线;
(2)若OA= ![]() CE,求∠ACB的大小.
CE,求∠ACB的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com