
【题目】从编号为1,2,3,4,…,10的10个大小、形状相同的小球中,任取5个球.如果某两个球的编号相邻,则称这两个球为一组“好球”.
(1)求任取的5个球中至少有一组“好球”的概率;
(2)在任取的5个球中,记“好球”的组数为X,求随机变量X的概率分布列和均值E(X).
科目:高中数学 来源: 题型:
【题目】已知F1,F2为椭圆E:![]() 的左、右焦点,且|F1F2|=2
的左、右焦点,且|F1F2|=2![]() ,点
,点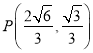 在E上.
在E上.
(1)求E的方程;
(2)直线l与以E的短轴为直径的圆相切,l与E交于A,B两点,O为坐标原点,试判断O与以AB为直径的圆的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,过焦点
,过焦点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,且当直线
两点,且当直线![]() 倾斜角为
倾斜角为![]() 时,与抛物线相交所得弦的长度为8.
时,与抛物线相交所得弦的长度为8.
(1)求抛物线![]() 的方程;
的方程;
(2)若分别过点![]() ,
,![]() 两点作抛物线
两点作抛物线![]() 的切线
的切线![]() ,
,![]() ,两条切线相交于点
,两条切线相交于点![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,判断四边形
,判断四边形![]() 是否存在外接圆,如果存在,求出外接圆面积的最小值;如果不存在,请说明理由.
是否存在外接圆,如果存在,求出外接圆面积的最小值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市管辖的海域内有一圆形离岸小岛,半径为1公里,小岛中心O到岸边AM的最近距离OA为2公里.该市规划开发小岛为旅游景区,拟在圆形小岛区域边界上某点B处新建一个浴场,在海岸上某点C处新建一家五星级酒店,在A处新建一个码头,且使得AB与AC满足垂直且相等,为方便游客,再建一条跨海高速通道OC连接酒店和小岛,设![]() .
.
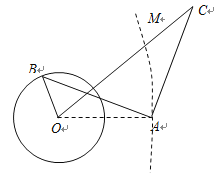
(1)设![]() ,试将
,试将![]() 表示成
表示成![]() 的函数;
的函数;
(2)若OC越长,景区的辐射功能越强,问当![]() 为何值时OC最长,并求出该最大值.
为何值时OC最长,并求出该最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过
,过![]() 的焦点且垂直于
的焦点且垂直于![]() 轴的直线被
轴的直线被![]() 截得的弦长为
截得的弦长为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过右焦点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴相交于点
轴相交于点![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中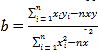 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将“□”和“○”按照如下规律从左到右进行排列:若每一个“□”或“○”占1个位置,即上述图形中,第1位是“□”,第4位是“○”,第7位是 “□”,则在第2017位之前(不含第2017位),“○”的个数为( )
□,○,□,○,○,○,□,○,○,○,○,○,□,○,○,○,○,○,○,○![]()
A.1970B.1971C.1972D.1973
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com