练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某城市随机抽取一个月（天）的空气质量指数监测数据，统计结果如下：


     
     
     
     
     
     
     
     
    空气质量
         		优
         		良
         		轻微污染
         		轻度污染
         		中度污染
         		中重度污染
         		重度污染
     
    天数
     
     
     
     
     
     
     
     
     
    （1）根据以上数据估计该城市这天空气质量指数的平均值；
    （2）若该城市某企业因空气污染每天造成的经济损失（单位：元）与空气质量指数（记为）的
    关系式为

    若在本月天中随机抽取一天，试估计该天经济损失大于元且不超过元的概率.

    （1）；（2）.

    解析试题分析：（1）将每组的中点值乘以相应的天数，求和后再除以总的天数即可求出的平均值；（2）利用结合分段函数的解析式求出的取值范围，从而确定相应的的天数，从而确定相应事件的概率.
    （1）该城市这30天空气质量指数的平均值为
    ；
    （2）设“在本月天中随机抽取一天，该天经济损失大于元且不超过元”为事件，
    由得，
    根据表格数据得共有天，
    所以.
    考点：1.平均数；2.古典概型

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：

    （1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；
    （2）求频率分布直方图中的a，b的值；
    （3）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的100名学生该周课外阅读时间的平均数在第几组（只需写出结论）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2013年11月，青岛发生输油管道爆炸事故造成胶州湾局部污染．国家海洋局用分层抽样的方法从国家环保专家、海洋生物专家、油气专家三类专家库中抽取若干人组成研究小组赴泄油海域工作，有关数据见表1（单位：人）

    海洋生物专家为了检测该地受污染后对海洋动物身体健康的影响，随机选取了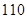只海豚进行了检测，并将有关数据整理为不完整的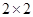列联表，如表2.
    （1）求研究小组的总人数；
    （2）写出表2中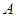、、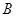、、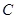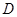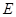的值，并判断有多大的把握认为海豚身体不健康与受到污染有关；
    （3）若从研究小组的环保专家和海洋生物专家中随机选人撰写研究报告，求其中恰好有人为环保专家的概率.
    附：①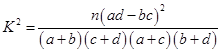，其中.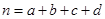
    ②















     

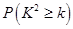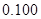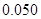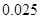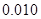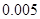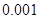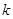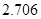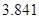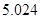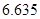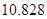    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品，现用两种新配方（分别称为A配方和B配方）做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：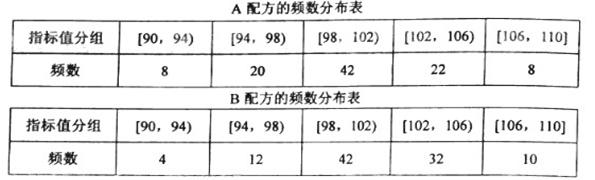

    （1）分别估计用A配方，B配方生产的产品的优质品率；
    （2）已知用B配方生成的一件产品的利润y(单位：元)与其质量指标值t的关系式为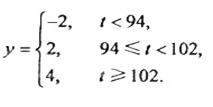

    从用B配方生产的产品中任取一件，其利润记为X（单位：元），求X的分布列及数学期望.（以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分12分 ）
    2013年国庆期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段，，，，，后得到如下图的频率分布直方图.
    （1）此调查公司在采样中,用到的是什么抽样方法?
    （2）求这40辆小型车辆车速的中位数的估计值；
    （3）若从车速在的车辆中任抽取3辆,求抽出的3辆车中车速在的车辆数的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    “根据《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80 mg/100ml（不含80）之间，属于酒后驾车，血液酒精浓度在80mg/100ml（含80）以上时，属醉酒驾车．”某市交警在该市一交通岗前设点对过往的车辆进行抽查，经过一晚的抽查，共查出酒后驾车者60名，图甲是用酒精测试仪对这60 名酒后驾车者血液中酒精浓度进行检测后依所得结果画出的频率分布直方图．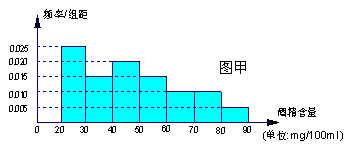

    （1）统计方法中，同一组数据常用该组区间的中点值作为代表，图乙的程序框图是对这60名酒后驾车者血液的酒精浓度做进一步的统计，求出图乙输出的S的值，并说明S的统计意义；（图乙中数据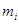与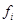分别表示图甲中各组的组中值及频率）

    （2）本次行动中，吴、李两位先生都被酒精测试仪测得酒精浓度属于70～90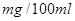的范围，但他俩坚称没喝那么多，是测试仪不准，交警大队队长决定在被酒精测试仪测得酒精浓度属于70～90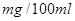范围的酒后驾车者中随机抽出2人抽血检验，设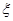为吴、李两位先生被抽中的人数，求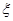的分布列，并求吴、李两位先生至少有1人被抽中的概率；

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某校高三有四个班，某次数学测试后，学校随机地在各班抽取部分学生进行测试成绩统计，各班被抽取的学生人数恰好成等差数列，人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示，其中120~130（包括120分但不包括130分）的频率为0.05，此分数段的人数为5人.
    （1）问各班被抽取的学生人数各为多少人？
    （2）求平均成绩；
    （3）在抽取的所有学生中，任取一名学生，求分数不低于90分的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知某地每单位面积菜地年平均使用氮肥量x(kg)与每单位面积蔬菜年平均产量y(t)之间的关系有如下数据：

    年份
    		1985
    		1986
    		1987
    		1988
    		1989
    		1990
    		1991
    		1992
    x(kg)
    		70
    		74
    		80
    		78
    		85
    		92
    		90
    		95
    y(t)
    		5.1
    		6.0
    		6.8
    		7.8
    		9.0
    		10.2
    		10.0
    		12.0
     
    年份
    		1993
    		1994
    		1995
    		1996
    		1997
    		1998
    		1999
    		 
    x(kg)
    		92
    		108
    		115
    		123
    		130
    		138
    		145
    		 
    y(t)
    		11.5
    		11.0
    		11.8
    		12.2
    		12.5
    		12.8
    		13.0
    		 
    (1)求x与y之间的相关系数，并检验是否线性相关；
    (2)若线性相关，求蔬菜产量y与使用氮肥量x之间的回归直线方程，并估计每单位面积施肥150 kg时，每单位面积蔬菜的年平均产量．
    (已知数据：＝101，≈10.113 3，＝161 125，＝1 628.55，＝16 076.8)

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    从某居民区随机抽取10个家庭,获得第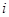个家庭的月收入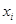(单位:千元)与月储蓄(单位:千元)的数据资料,算得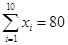
    ,,,.
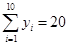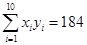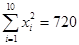    (1)求家庭的月储蓄对月收入的线性回归方程;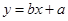
    (2)判断变量与之间是正相关还是负相关;
    (3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
    其中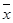,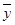为样本平均值,线性回归方程也可写为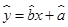
    附:线性回归方程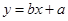中,,,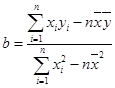

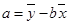    查看答案和解析>>

    同步练习册答案