
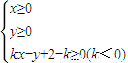 所表示的平面区域的面积最小时,实数k的值为( )
所表示的平面区域的面积最小时,实数k的值为( )

 •|OA|•|OB|=
•|OA|•|OB|= •|2-k|•|1-
•|2-k|•|1- |.
|. (4-k-
(4-k-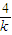 )=
)= [4+(-k)+(-
[4+(-k)+(-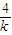 )]≥
)]≥ [4+2
[4+2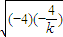 ]=4,
]=4,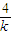 ,解得k=-2.
,解得k=-2.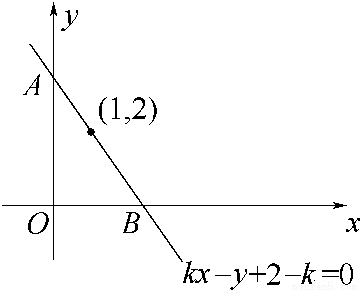


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:2014届吉林省高二上学期期中考试数学试卷(解析版) 题型:选择题
当不等式组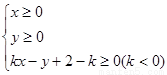 所表示的平面区域的面积最小时,实数k的值为( )
所表示的平面区域的面积最小时,实数k的值为( )
A.-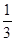 B.-
B.-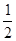 C.-1 D.-2
C.-1 D.-2
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省临沂市高三上学期期中考试文科数学卷 题型:选择题
设不等式组 所表示的平面区域是
所表示的平面区域是 ,平面区
,平面区
域 与
与 关于原点对称,对于
关于原点对称,对于 中的任意点A与
中的任意点A与 中的任意点B,|AB|的最小值等于
中的任意点B,|AB|的最小值等于
(A) (B)2
(B)2 (C)
(C) (D)3
(D)3
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省临沂市高三上学期期中考试文科数学卷 题型:选择题
设不等式组 所表示的平面区域是
所表示的平面区域是 ,平面区
,平面区
域 与
与 关于原点对称,对于
关于原点对称,对于 中的任意点A与
中的任意点A与 中的任意点B,|AB|的最小值等于
中的任意点B,|AB|的最小值等于
(A) (B)2
(B)2 (C)
(C) (D)3
(D)3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com