练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为了得到函数y=sin（2x﹣ ）的图象，只需把函数y=sin2x的图象上所有的点（ ）
    A.向左平行移动 个单位长度
    B.向右平行移动 个单位长度
    C.向左平行移动 个单位长度
    D.向右平行移动 个单位长度

    【答案】D
    【解析】解：把函数y=sin2x的图象向右平移 个单位长度，可得函数y=sin2（x﹣ ）=sin（2x﹣ ）的图象，

    故选：D．

    【考点精析】根据题目的已知条件，利用函数y=Asin（ωx+φ）的图象变换的相关知识可以得到问题的答案，需要掌握图象上所有点向左（右）平移个单位长度，得到函数的图象；再将函数的图象上所有点的横坐标伸长（缩短）到原来的倍（纵坐标不变），得到函数的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的倍（横坐标不变），得到函数的图象．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜ ）的部分图象如图所示．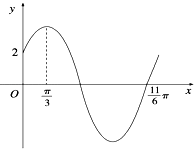
    （1）求f（x）的解析式；
    （2）将函数y=f（x）的图象上所有点的纵坐标不变，横坐标缩短为原来的 倍，再将所得函数图象向右平移 个单位，得到函数y=g（x）的图象，求g（x）的单调递增区间；
    （3）当x∈[﹣ ， ]时，求函数y=f（x+ ）﹣ f（x+ ）的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直三棱柱ABC﹣A1B1C1中，D，E分别是BC，A1B1的中点．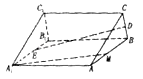
    （1）求证：DE∥平面ACC1A1；
    （2）设M为AB上一点，且AM= AB，若直三棱柱ABC﹣A1B1C1的所有棱长均相等，求直线DE与直线A1M所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=（2x﹣2）2+（2﹣x+2）2﹣10在区间[1，2]上的最大值与最小值之积为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知半径为 ，圆心在直线l1：x﹣y+1=0上的圆C与直线l2： x﹣y+1﹣ =0相交于M，N两点，且|MN|=
    （1）求圆C的标准方程；
    （2）当圆心C的横、纵坐标均为整数时，若对任意m∈R，直线l3：mx﹣y+ +1=0与圆C恒有公共点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，平面内有三个向量 ， ， ，其中 与 的夹角为30°， 与 的夹角为90°，且| |=2，| |=2，| |=2 ，若 =λ +μ ，（λ，μ∈R）则（ ）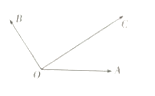
    A.λ=4，μ=2
    B.λ=4，μ=1
    C.λ=2，μ=1
    D.λ=2，μ=2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|x2﹣3x﹣10＜0}，B={x|m+1≤x≤2m﹣1}．
    （1）当m=3时，求集合（UA）∩B；
    （2）若A∩B=B，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求与圆（x﹣2）2+y2=2相切且在x轴，y轴上截距相等的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体ABCD﹣A1B1C1D1 ， 则下列四个命题：
    ①P在直线BC1上运动时，三棱锥A﹣D1PC的体积不变；
    ②P在直线BC1上运动时，直线AP与平面ACD1所成角的大小不变；
    ③P在直线BC1上运动时，二面角P﹣AD1﹣C的大小不变；
    ④M是平面A1B1C1D1上到点D和C1距离相等的点，则M点的轨迹是过D1点的直线
    其中真命题的个数是（ ）

    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    同步练习册答案