
 在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设
在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设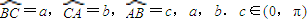 ,二面角B-OA-C、
,二面角B-OA-C、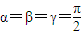 ,则球面三角形ABC的面积为
,则球面三角形ABC的面积为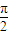 ;
;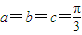 ,则四面体OABC的侧面积为
,则四面体OABC的侧面积为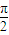 ;
;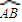 在点A处的切线l1与圆弧
在点A处的切线l1与圆弧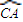 在点A处的切线l2的夹角等于a;
在点A处的切线l2的夹角等于a;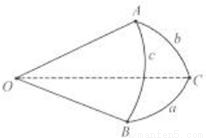
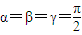 ,知球面三角形ABC是
,知球面三角形ABC是 球体,故球面三角形ABC的面积=
球体,故球面三角形ABC的面积= =
= ;由
;由 ,知四面体OABC的面积=3×
,知四面体OABC的面积=3×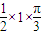 =
=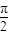 ,;圆弧
,;圆弧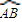 在点A处的切线l1在OAB面上与OA垂直,圆弧
在点A处的切线l1在OAB面上与OA垂直,圆弧 在点A处的切线l2在OAC面上与OA垂直,故l1与l2夹角等于α;若a=b,则α=β.
在点A处的切线l2在OAC面上与OA垂直,故l1与l2夹角等于α;若a=b,则α=β. ,
, 球体,
球体, =
= .
. ,
,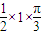 =
= ,
,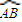 在点A处的切线l1在OAB面上与OA垂直,
在点A处的切线l1在OAB面上与OA垂直, 在点A处的切线l2在OAC面上与OA垂直,
在点A处的切线l2在OAC面上与OA垂直,

 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
| PC |
| PA |
| PB |
| AP |
| AB |
| AQ |
| AC |
| 1 |
| m |
| 1 |
| n |

查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•成都一模)如图,设A、B、C是球O面上的三点,我们把大圆的劣弧
(2010•成都一模)如图,设A、B、C是球O面上的三点,我们把大圆的劣弧 |
| BC |
 |
| CA |
 |
| AB |
 |
| BC |
 |
| CA |
 |
| AB |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
 |
| AB |
 |
| CA |
查看答案和解析>>
科目:高中数学 来源:2010年四川省成都市高考数学一模试卷(文科)(解析版) 题型:解答题
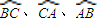 在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设
在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设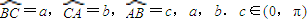 ,二面角B-OA-C、
,二面角B-OA-C、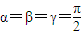 ,则球面三角形ABC的面积为
,则球面三角形ABC的面积为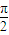 ;
; ,则四面体OABC的侧面积为
,则四面体OABC的侧面积为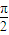 ;
;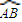 在点A处的切线l1与圆弧
在点A处的切线l1与圆弧 在点A处的切线l2的夹角等于a;
在点A处的切线l2的夹角等于a;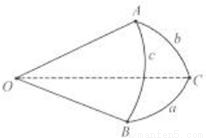
查看答案和解析>>
科目:高中数学 来源:2010年安徽省宿州市灵璧中学高考压轴数学试卷1(理科)(解析版) 题型:解答题
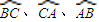 在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设
在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设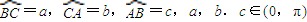 ,二面角B-OA-C、
,二面角B-OA-C、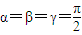 ,则球面三角形ABC的面积为
,则球面三角形ABC的面积为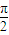 ;
;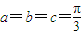 ,则四面体OABC的侧面积为
,则四面体OABC的侧面积为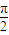 ;
;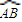 在点A处的切线l1与圆弧
在点A处的切线l1与圆弧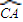 在点A处的切线l2的夹角等于a;
在点A处的切线l2的夹角等于a;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com