
【题目】已知定义在R的奇函数![]() 满足
满足![]() ,且
,且![]() 时,
时, ![]() ,下面四种说法①
,下面四种说法①![]() ;②函数
;②函数![]() 在[-6,-2]上是增函数;③函数
在[-6,-2]上是增函数;③函数![]() 关于直线
关于直线![]() 对称;④若
对称;④若![]() ,则关于
,则关于![]() 的方程
的方程![]() 在[-8,8]上所有根之和为-8,其中正确的序号__________。
在[-8,8]上所有根之和为-8,其中正确的序号__________。
【答案】①④
【解析】取x=1,得f(14)=f(3)=f(1)=log2(1+1)=1,,所以f(3)=f(3)=1,故①正确;
定义在R上的奇函数f(x)满足f(x4)=f(x),则f(x4)=f(x),
∴f(x2)=f(x2),
∴函数f(x)关于直线x=2对称,
由于函数对称中心原点(0,0)的对称点为(4,0),故函数f(x)也关于(4,0)点对称,故③不正确;
∵x∈[0,2]时,f(x)=log2(x+1)为增函数,
由奇函数在对称区间上单调性相同可得,x∈[2,0]时,函数为单调增函数,
∴x∈[2,2]时,函数为单调增函数,
∵函数f(x)关于直线x=2对称,∴函数f(x)在[6,2]上是减函数,故②不正确;
若m∈(0,1),则关于x的方程f(x)m=0在[8,8]上有4个根,其中两根的和为6×2=12,另两根的和为2×2=4,所以所有根之和为8.故④正确
故答案为:①④


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=2![]() sinxcosx+2cos2x﹣1.
sinxcosx+2cos2x﹣1.
(1)求f(x)的最大值,以及该函数取最大值时x的取值集合;
(2)在△ABC中,a、b、c分别是角A、B、C所对的边长,且![]() ,求角C.
,求角C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x∈R),给出下面四个命题:
(x∈R),给出下面四个命题:
①函数f(x)的图象一定关于某条直线对称;
②函数f(x)在R上是周期函数;
③函数f(x)的最大值为 ![]() ;
;
④对任意两个不相等的实数 ![]() ,都有
,都有 ![]() 成立.
成立.
其中所有真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() (p、q为常数,
(p、q为常数, ![]() ),又
),又![]() ,
, ![]() ,
, ![]() .
.
(1)求p、q的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在正整数m、n,使![]() 成立?若存在,求出所有符合条件的有序实数对
成立?若存在,求出所有符合条件的有序实数对![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(2ωx+ ![]() )(其中ω>0),且f(x)的图象在y轴右侧的第一个最高点的横坐标是
)(其中ω>0),且f(x)的图象在y轴右侧的第一个最高点的横坐标是 ![]() .
.
(1)求y=f(x)的最小正周期及对称轴;
(2)若x∈ ![]() ,函数
,函数 ![]() ﹣af(x)+1的最小值为0.求a的值.
﹣af(x)+1的最小值为0.求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题12分)已知平行四边形![]() 的三个顶点的坐标为
的三个顶点的坐标为![]() ,
,![]() ,
,![]() .
.
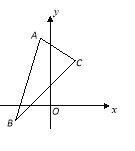
(Ⅰ)在![]() ABC中,求边AC中线所在直线方程;
ABC中,求边AC中线所在直线方程;
(Ⅱ)求平行四边形![]() 的顶点D的坐标及边BC的长度;
的顶点D的坐标及边BC的长度;
(Ⅲ)求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正四棱锥P﹣ABCD中,侧棱PA与底面ABCD所成的角的正切值为![]() .
.
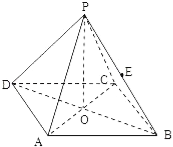
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,求异面直线PD与AE所成角的正切值;
(3)问在棱AD上是否存在一点F,使EF⊥侧面PBC,若存在,试确定点F的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 数列{an}满足,2Sn=an(an+1).
(1)求数列{an}的通项公式;
(2)设数列{ ![]() }的前n项和为An , 求证:对任意正整数n,都有An<
}的前n项和为An , 求证:对任意正整数n,都有An< ![]() 成立;
成立;
(3)数列{bn}满足bn=( ![]() )nan , 它的前n项和为Tn , 若存在正整数n,使得不等式(﹣2)n﹣1λ<Tn+
)nan , 它的前n项和为Tn , 若存在正整数n,使得不等式(﹣2)n﹣1λ<Tn+ ![]() ﹣2n﹣1成立,求实数λ的取值范围.
﹣2n﹣1成立,求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com