
分析 (1)根据指数幂和对数之间的关系,结合对数的换底公式即可求$\frac{1}{a}+\frac{1}{b}$的值
(2)求函数y=(2x2-1)(3x+1)的导数.
解答 解:(1)若2a=5b=10,则a=log210,b=log510,
则$\frac{1}{a}+\frac{1}{b}$=$\frac{1}{lo{g}_{2}10}+\frac{1}{lo{g}_{5}10}$=lg2+lg5=lg(2×5)=lg10=1.
(2)∵函数y=(2x2-1)(3x+1).
∴y′=4x(3x+1)+3(2x2-1)=18x2+4x-3.
点评 本题主要考查对数的基本运算以及函数的导数的计算,考查学生的运算能力.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
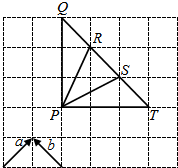 如图所示,下列结论正确的是( )
如图所示,下列结论正确的是( )| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com