
����Ŀ������������12����ijʳƷ��Ϊ�˼��һ���Զ���װ��ˮ�ߵ���������������ȡ����ˮ����![]() ����Ʒ��Ϊ�����Ƴ����ǵ���������λ�������������ķ�������Ϊ
����Ʒ��Ϊ�����Ƴ����ǵ���������λ�������������ķ�������Ϊ![]() ��
��![]() �� ��
�� ��![]() ���ɴ˵õ�������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��
���ɴ˵õ�������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��
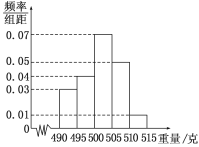
��1������Ƶ�ʷֲ�ֱ��ͼ������������![]() �˵IJ�Ʒ������
�˵IJ�Ʒ������
��2����������ȡ��![]() ����Ʒ����ȡ
����Ʒ����ȡ![]() ������
������![]() ��������
Ϊ��������![]() �˵IJ�Ʒ��������
�˵IJ�Ʒ��������![]() �ķֲ��У�
�ķֲ��У�
��3���Ӹ���ˮ������ȡ![]() ����Ʒ����ǡ��
����Ʒ����ǡ��![]() ����Ʒ����������
����Ʒ����������![]() �˵ĸ��ʣ�
�˵ĸ��ʣ�
���𰸡���1��![]() ��������
��������
��2��Y�ķֲ���Ϊ
| 0 | 1 | 2 |
P |
|
|
|
��3��![]() .
.
��������
�����������1������Ƶ�ʷֲ�ֱ��ͼ�����������2����![]() �ķֲ��У�����
�ķֲ��У�����![]() Ϊ��������
Ϊ��������![]() �˵IJ�Ʒ��������ȡ��
�˵IJ�Ʒ��������ȡ��![]() ����Ʒ����ȡ
����Ʒ����ȡ![]() �������
�������![]() �Ŀ���ȡֵΪ0,1,2.�ɹŵ���͵ĸ������ֱ�������ʣ����÷ֲ��У���3���Ӹ���ˮ������ȡ
�Ŀ���ȡֵΪ0,1,2.�ɹŵ���͵ĸ������ֱ�������ʣ����÷ֲ��У���3���Ӹ���ˮ������ȡ![]() ����Ʒ����ǡ��
����Ʒ����ǡ��![]() ����Ʒ����������
����Ʒ����������![]() �˵ĸ���������϶���ֲ������ö���ֲ���������ǡ��
�˵ĸ���������϶���ֲ������ö���ֲ���������ǡ��![]() ����Ʒ����������
����Ʒ����������![]() �˵ĸ���.
�˵ĸ���.
�����������1������Ƶ�ʷֲ�ֱ��ͼ��֪����������505�˵IJ�Ʒ����Ϊ
![]() �������� ��/span>2����
�������� ��/span>2����
��2��![]() �Ŀ���ȡֵΪ0,1,2. ��3����
�Ŀ���ȡֵΪ0,1,2. ��3����
![]() ��4����
��4����
![]() ��5����
��5����
![]() ��6����
��6����
Y�ķֲ���Ϊ
| 0 | 1 | 2 |
P |
|
|
|
��3�����������������壬����ˮ���ϲ�Ʒ��������505�˵ĸ���Ϊ0.3 ��8����
��![]() Ϊ��ȡ��5����Ʒ����������505�˵IJ�Ʒ������
Ϊ��ȡ��5����Ʒ����������505�˵IJ�Ʒ������
��![]() �� ��10����
�� ��10����
���������Ϊ![]() ��12����
��12����


 �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д� �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCD��ƽ���ı��Σ���BCD=135�㣬����PAB�͵���ABCD����BAP=90�㣬AB=AC=PA=2��E��F�ֱ�ΪBC��AD���е㣬��M���߶�PD�ϣ� 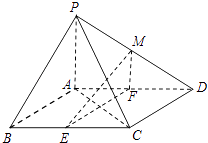
��1����֤��EF��ƽ��PAC��
��2�����ֱ��ME��ƽ��PBC���ɵĽǺ�ֱ��ME��ƽ��ABCD���ɵĽ���ȣ��� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017ɽ��Т�忼ǰ��������֪����![]() (
(![]() �dz���),
�dz���),
��1������![]() �ĵ������䣻
�ĵ������䣻
��2����![]() ʱ������
ʱ������![]() ����㣬��
����㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ������
������![]() ��
�� ![]() ����Ȼ�����ĵ���.
����Ȼ�����ĵ���.
������![]() ��
��![]() �ϵ�����������
�ϵ�����������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ��֤����
��֤���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���BAC=120�㣬AC=3����ABC��������� ![]() ��DΪ�߳�BC��һ�㣮
��DΪ�߳�BC��һ�㣮 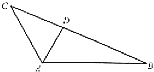
��1����BC�ij���
��2����AD= ![]() ʱ����cos��CAD��ֵ��
ʱ����cos��CAD��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���y=f��x���������x������f��x+1��=��f��x��������1��x��1ʱ��f��x��=x3 �� ������g��x��=f��x����loga|x|����6����㣬��aȡֵ��Χ�ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������14�֣�
����ABC�����ڽ�A��B��C���Եı߷ֱ�Ϊa��b��c. ��֪C��![]() ��acosA=bcosB��
��acosA=bcosB��
��1�����A�Ĵ�С��
��2����ͼ������ABC�������ACD��ȡһ��P��ʹ��PC��2������P�ֱ���ֱ��CA��CD�Ĵ���PM��PN������ֱ���M��N������PCA��������PM��PN�����ֵ����ʱ����ȡֵ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ԥ��˵��δ������ÿ������ĸ��ʶ���0.6����1��2��3��4��ʾ�����꣬��5��6��7��8��9��0��ʾ���꣬���ü������������20�����������δ������ǡ����������ĸ��ʴ�Լ�� ��
757 220 582 092 103 000 181 249 414 993
010 732 680 596 761 835 463 521 186 289��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���˹�˾��A��B�����ͺŵij����е��ס������ؼ�ij�;����ҵ��ÿ��ÿ������һ�Σ�A��B���ֳ������ؿ����ֱ�Ϊ36�˺�60�ˣ��Ӽ�ȥ�ҵص�Ӫ�˳ɱ��ֱ�Ϊ1600Ԫ/����2400Ԫ/������˾���齨һ��������21�����Ŀ��˳��ӣ���Ҫ��B�ͳ�������A�ͳ�7������ÿ��Ҫ�Բ�����900������Ӽ�ȥ�ҵص��ÿͣ���ʹ��˾�Ӽ�ȥ�ҵص�Ӫ�˳ɱ���С����ôӦ�䱸A�ͳ���B�ͳ�����������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com