已知f(x)=2x3+ax2+bx+c在x=-1处取得极值8,又x=2时,f(x) 也取得极值.
(1)求a,b,c的值,写出f(x)的解析式;(2)求f(x)的单调区间.
【答案】
分析:(1)先求出导函数,由题意可知,x=-1,x=2是方程6x
2+2ax+b=0的两根,利用根与系数的关系可求出a和b,最后由x=-1时f(x)的极值是8求出c,从而求出函数的解析式;
(2)先求出导函数,令f′(x)=0求出极值点,根据满足f′(x)>0的是单调增区间,满足f′(x)<0的是单调减区间,即可求出所求.
解答:解:(1)f′(x)=6x
2+2ax+b,由题意可知,x=-1,x=2是方程6x
2+2ax+b=0的两根,
故:x
1+x
2═
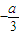
=1,∴a=-3,-2=
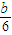
,∴b=-12,又,当x=-1时f(x)的极值是8,
∴c=1∴f(x)=2x
3-3x
2-12x+1 (6分)
(2)∵f′(x)=6x
2-6x-12,令f′(x)=0,即6x
2-6x-12=0,∴x=2或x=-1,
解得函数的单调区间为:增区间为:(-∞,-1),(2,+∞)
单调减区间为(-1,2)(6分)
点评:本题主要考查了函数在某点取极值的条件,同时考查了利用导数研究函数的单调性,属于中档题.

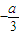 =1,∴a=-3,-2=
=1,∴a=-3,-2=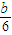 ,∴b=-12,又,当x=-1时f(x)的极值是8,
,∴b=-12,又,当x=-1时f(x)的极值是8,

 智能训练练测考系列答案
智能训练练测考系列答案