
已知函数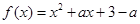 ,其中
,其中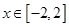 。
。
(1)当a=1时,求它的单调区间;
(2)当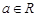 时,讨论它的单调性;
时,讨论它的单调性;
(3)若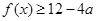 恒成立,求
恒成立,求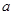 的取值范围.
的取值范围.
(1)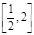 (2)当
(2)当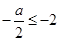 得
得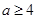 ,
,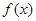 单调增区间为
单调增区间为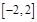 ;当
;当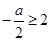 得
得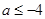 ,
,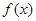 单调减区间为
单调减区间为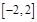 ;当
;当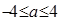 时,
时,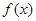 单调增区间为
单调增区间为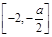 ,单调减区间为
,单调减区间为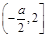 . (3)
. (3)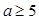
解析试题分析:(1)当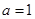 时,
时,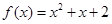 ,对称轴方程为
,对称轴方程为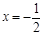 ,
,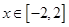 在对称轴方程
在对称轴方程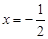 内,则
内,则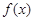 的单调减区间为
的单调减区间为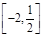 ;
;
单调减区间为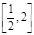 5分
5分
(2)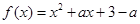 ,对称轴方程为
,对称轴方程为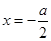 ,
,
下面分三种情况讨论:
当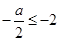 得
得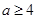 ,
,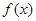 单调增区间为
单调增区间为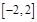 ;
;
当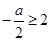 得
得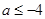 ,
,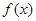 单调减区间为
单调减区间为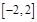 ;
;
当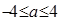 时,
时,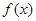 单调增区间为
单调增区间为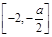 ,单调减区间为
,单调减区间为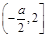 . 10分
. 10分
(3)当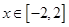 时,有
时,有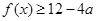 恒成立,
恒成立,
等价于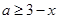 ,只要
,只要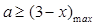 ,
,
而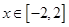 ,
,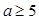 15分
15分
考点:本题考查了函数的性质
点评:对于二次函数f(x)=ax2+bx+c=0(a≠0)在实数集R上恒成立问题可利用判别式直接求解,即 f(x)>0恒成立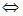

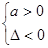 ;f(x)<0恒成立
;f(x)<0恒成立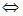

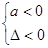 .若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解.
.若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:解答题
若函数 都在区间
都在区间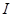 上有定义,对任意
上有定义,对任意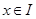 ,都有
,都有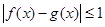 成立,则称函数
成立,则称函数 为区间
为区间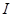 上的“伙伴函数”
上的“伙伴函数”
(1)若 为区间
为区间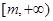 上的“伙伴函数”,求
上的“伙伴函数”,求 的范围。
的范围。
(2)判断 是否为区间
是否为区间 上的“伙伴函数”?
上的“伙伴函数”?
(3)若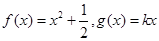 为区间
为区间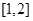 上的“伙伴函数”,求
上的“伙伴函数”,求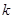 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数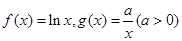 ,设
,设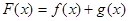
(1)求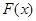 的单调区间;
的单调区间;
(2)若以 图象上任意一点
图象上任意一点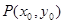 为切点的切线的斜率
为切点的切线的斜率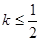 恒成立,求实数
恒成立,求实数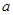 的最小值;
的最小值;
(3)是否存在实数 ,使得函数
,使得函数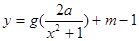 的图象与
的图象与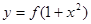 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于定义在实数集 上的两个函数
上的两个函数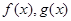 ,若存在一次函数
,若存在一次函数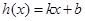 使得,对任意的
使得,对任意的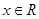 ,都有
,都有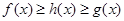 ,则把函数
,则把函数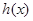 的图像叫函数
的图像叫函数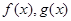 的“分界线”。现已知
的“分界线”。现已知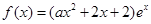 (
(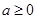 ,
,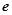 为自然对数的底数),
为自然对数的底数),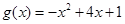
(1)求 的递增区间;
的递增区间;
(2)当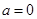 时,函数
时,函数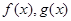 是否存在过点
是否存在过点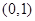 的“分界线”?若存在,求出函数
的“分界线”?若存在,求出函数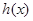 的解析式,若不存在,请说明理由。
的解析式,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,
OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交
于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.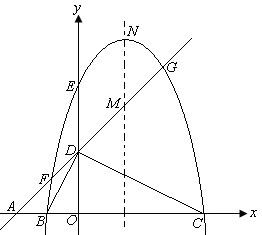
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件
的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成
为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com