
 ,以此类推蚂蚁第一次爬完之后在A点的概率为0,得到结果.
,以此类推蚂蚁第一次爬完之后在A点的概率为0,得到结果.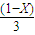 ①
① ②
② ③
③ ④
④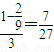


科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源:2008年江苏省南通市通州区兴仁中学高二期末数学模拟试卷(解析版) 题型:填空题
 ;由以上平面图形的特性类比空间图形:设正四面体ABCD的棱长为a,P是正四面体ABCD内的任意一点,且P到四个面ABC、ABD、ACD、BCD的距离分别为d1,d2,d3,d4,则有d1+d2+d3+d4为定值 .
;由以上平面图形的特性类比空间图形:设正四面体ABCD的棱长为a,P是正四面体ABCD内的任意一点,且P到四个面ABC、ABD、ACD、BCD的距离分别为d1,d2,d3,d4,则有d1+d2+d3+d4为定值 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com