
【题目】【2017河北唐山三模】已知函数![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 在区间
在区间![]() 有唯一零点
有唯一零点![]() ,证明:
,证明: ![]() .
.
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)求导得![]() , 分
, 分![]() ,
, ![]() ,
, ![]() ,三种情况讨论可得单调区间.
,三种情况讨论可得单调区间.
(Ⅱ)由(1)及![]() 可知:仅当极大值等于零,即
可知:仅当极大值等于零,即![]() 且
且 ![]()
所以![]() ,且
,且![]() ,消去
,消去![]() 得
得![]() ,构造函数,证明单调且零点存在且唯一即可.
,构造函数,证明单调且零点存在且唯一即可.
试题解析:(Ⅰ) ![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,
,
若![]() ,即
,即![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
若![]() ,即
,即![]() ,则
,则![]() ,仅当
,仅当![]() 时,等号成立,
时,等号成立,
当![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
若![]() ,即
,即![]() ,则
,则![]() 有两个零点
有两个零点![]() ,
, ![]() ,
,
由![]() ,
, ![]() 得
得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增.
单调递增.
综上所述,
当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在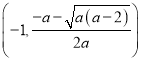 和
和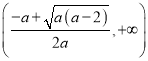 上单调递增,
上单调递增,
在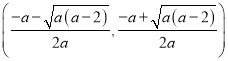 上单调递减.
上单调递减.
(Ⅱ)由(1)及![]() 可知:仅当极大值等于零,即
可知:仅当极大值等于零,即![]() 时,符合要求.
时,符合要求.
此时, ![]() 就是函数
就是函数![]() 在区间
在区间![]() 的唯一零点
的唯一零点![]() .
.
所以![]() ,从而有
,从而有![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
令![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
再由(1)知: ![]() ,
, ![]() ,
, ![]() 单调递减,
单调递减,
又因为![]() ,
, ![]() ,
,
所以![]() ,即
,即![]()


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的一条直线与抛物线
的一条直线与抛物线![]() 交于
交于![]() 两点,若抛物线在
两点,若抛物线在![]() 两点的切线交于点
两点的切线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
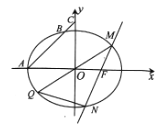
【题目】【2017重庆二诊】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过点
,过点![]() 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,
, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,连接
两点,连接![]() (
(![]() 为坐标原点)并延长交椭圆
为坐标原点)并延长交椭圆![]() 于点
于点![]() ,求
,求![]() 面积的最大值及取最大值时直线
面积的最大值及取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为备战![]() 年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得
年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得![]() 分,负者得
分,负者得![]() 分,在每一场比赛中,甲胜乙的概率为
分,在每一场比赛中,甲胜乙的概率为![]() ,丙胜甲的概率为
,丙胜甲的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为
,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)设在该次对抗比赛中,丙得分为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)
在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的上顶点到焦点的距离为2,离心率为
(a>b>0)的上顶点到焦点的距离为2,离心率为![]() .
.
(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣2ax+1+lnx
﹣2ax+1+lnx
(1)当a=0时,若函数f(x)在其图象上任意一点A处的切线斜率为k,求k的最小值,并求此时的切线方程;
(2)若函数f(x)的极大值点为x1 , 证明:x1lnx1﹣ax12>﹣1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com