
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>b>a |
分析 利用指数函数、对数函数的单调性求解.
解答 解:∵$a={2016^{\frac{1}{2017}}},b={log_{2016}}^{\sqrt{2017}},c={log_{2017}}^{\sqrt{2016}}$,
$a=201{6}^{\frac{1}{2017}}$>20160=1,
0=log20161>b=$lo{g}_{2016}\sqrt{2107}$>$lo{g}_{2016}\sqrt{2016}$=$\frac{1}{2}$,
c=$lo{g}_{2017}\sqrt{2016}$<$lo{g}_{2017}\sqrt{2017}$=$\frac{1}{2}$,
∴a>b>c.
a,b,c的大小关系为a>b>c.
故选:A.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意指数函数、对数函数的单调性的合理运用.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
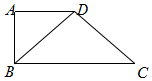 如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将
如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将| A. | 面ABD⊥面ABC | B. | 面ADC⊥面BDC | C. | 面ABC⊥面BDC | D. | 面ADC⊥面ABC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | 2 | C. | $\frac{2}{π}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com