
【题目】已知函数![]() 若关于
若关于![]() 的方程
的方程![]() 有且只有一个实数根,则实数k的取值范围是_____.
有且只有一个实数根,则实数k的取值范围是_____.
科目:高中数学 来源: 题型:
【题目】P是圆![]() 上的动点,P点在x轴上的射影是D,点M满足
上的动点,P点在x轴上的射影是D,点M满足![]() .
.
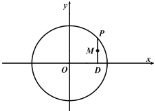
(1)求动点M的轨迹C的方程,并说明轨迹是什么图形;
(2)过点![]() 的直线l与动点M的轨迹C交于不同的两点A,B,求以OA,OB为邻边的平行四边形OAEB的顶点E的轨迹方程.
的直线l与动点M的轨迹C交于不同的两点A,B,求以OA,OB为邻边的平行四边形OAEB的顶点E的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月23日,在![]() 省
省![]() 市举办的2019年中国农民丰收节“新电商与农业科技创新”论坛上,来自政府相关部门的领导及11所中国高校的专家学者以“农业科技创新与乡村振兴”、“新农人与脱贫攻坚”为核心议题各抒己见,农产品方面的科技创新越来越成为21世纪大国崛起的一项重大突破.科学家对某农产品每日平均增重量
市举办的2019年中国农民丰收节“新电商与农业科技创新”论坛上,来自政府相关部门的领导及11所中国高校的专家学者以“农业科技创新与乡村振兴”、“新农人与脱贫攻坚”为核心议题各抒己见,农产品方面的科技创新越来越成为21世纪大国崛起的一项重大突破.科学家对某农产品每日平均增重量![]() (单位:
(单位:![]() )与每日营养液注射量
)与每日营养液注射量![]() (单位:
(单位:![]() )之间的关系统计出表1一组数据:
)之间的关系统计出表1一组数据:
表1
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3.5 | 5 | 6.6 | 8.4 |
(1)根据表1和表2的相关统计值求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)计算拟合指数![]() 的值,并说明线性回归模型的拟合效果(
的值,并说明线性回归模型的拟合效果(![]() 的值在.98以上说明拟合程度好);
的值在.98以上说明拟合程度好);
(3)若某日该农产品的营养液注释量为![]() ,预测该日这种农产品的平均增长重量(结果精确到0.1).
,预测该日这种农产品的平均增长重量(结果精确到0.1).
附:①
表2
|
|
|
|
92.4 | 55 | 25 | 0.04 |
②对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: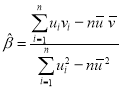 ,
,![]() ,
,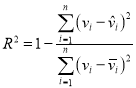 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两射线
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两射线![]() 、
、![]() 相互垂直,与曲线C分别相交于A、B两点(不同于点O),且
相互垂直,与曲线C分别相交于A、B两点(不同于点O),且![]() 的倾斜角为锐角
的倾斜角为锐角![]() .
.
(1)求曲线C和射线![]() 的极坐标方程;
的极坐标方程;
(2)求△OAB的面积的最小值,并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,将直线
,将直线![]() 绕极点
绕极点![]() 逆时针旋转
逆时针旋转![]() 个单位得到直线
个单位得到直线![]() .
.
(1)求![]() 和
和![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com