Question

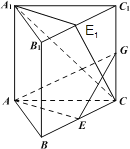
【题目】如图，在三棱柱中， 平面是BC的中点．

求证： ；

求异面直线AE与所成的角的大小；

若G为中点，求二面角的正切值．

Answer 1

【答案】见解析； .

【解析】试题分析： 由面ABC及线面垂直的性质可得，由是BC的中点，及等腰三角形三线合一，可得，结合线面垂直的判定定理可证得面，进而由线面垂直的性质得到；

取的中点，连，根据异面直线夹角定义可得， 是异面直线A与所成的角，设，解三角形可得答案．

连接AG，设P是AC的中点，过点P作于Q，连，则，由直三棱锥的侧面与底面垂直，结合面面垂直的性质定理，可得平面，进而由二面角的定义可得是二面角的平面角．

试题解析：

因为面面ABC，所以

由为BC的中点得到

面， .

解： 取的中点，连，

则，

是异面直线AE与所成的角

，则由，

可得

在中， -

所以异面直线AE与所成的角为-

连接AG，设P是AC的中点，过点P作于Q，连，则

又平面平面

平面-

而．

是二面角的平面角

由，得

所以二面角的平面角正切值是.