
【题目】如图,已知A,B,C为直角坐标系xOy中的三个定点
(Ⅰ)若点D为□ABCD的第四个顶点,求|![]() |;
|;
(Ⅱ)若点P在直线OC上,且![]() ·
·![]() =4,求点P的坐标.
=4,求点P的坐标.

【答案】(1)![]() .(2)(-1,1)或(4,-4).
.(2)(-1,1)或(4,-4).
【解析】试题分析:(1)由图得到点的坐标,根据点点距得到|![]() |=
|=![]() ;(2)根据向量坐标化得到
;(2)根据向量坐标化得到![]() ·
·![]() =(5+2λ)(1+2λ)+(3-2λ)(-3-2λ)=4,解得λ=
=(5+2λ)(1+2λ)+(3-2λ)(-3-2λ)=4,解得λ=![]() 或-2,从而得到点的坐标.
或-2,从而得到点的坐标.
解析:
(I)由图可知A(5,3),B(1,-3),C(-2,2),
所以,B=(4,6),BC=(-3,5),所以,|![]() |=|
|=|![]() +
+![]() |=
|=![]() =
=![]() .
.
(Ⅱ)因为点P在直线OC上,所以可设![]() =λ
=λ![]() =(-2λ,2λ),
=(-2λ,2λ),
所以,![]() =(5+2λ,3-2λ),
=(5+2λ,3-2λ),![]() =(1+2λ,-3-2λ),
=(1+2λ,-3-2λ),
所以,![]() ·
·![]() =(5+2λ)(1+2λ)+(3-2λ)(-3-2λ)=4,解得λ=
=(5+2λ)(1+2λ)+(3-2λ)(-3-2λ)=4,解得λ=![]() 或-2.
或-2.
故点P的坐标为(-1,1)或(4,-4).


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断并证明函数![]() 的奇偶性;
的奇偶性;
(2)判断当![]() 时函数
时函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)若![]() 定义域为
定义域为![]() ,解不等式
,解不等式![]() .
.
【答案】(1)奇函数(2)增函数(3)![]()
【解析】试题分析:(1)判断与证明函数的奇偶性,首先要确定函数的定义域是否关于原点对称,再判断f(-x)与f(x)的关系,如果对定义域上的任意x,都满足f(-x)=f(x)就是偶函数,如果f(-x)=-f(x)就是奇函数,否则是非奇非偶函数。(2)利函数单调性定义证明单调性,按假设,作差,化简,判断,下结论五个步骤。(3)由(1)(2)奇函数![]() 在(-1,1)为单调函数,
在(-1,1)为单调函数,
原不等式变形为f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函数的单调性及定义(-1,1)求解得x范围。
试题解析:(1)函数![]() 为奇函数.证明如下:
为奇函数.证明如下:
![]() 定义域为
定义域为![]()
又![]()
![]() 为奇函数
为奇函数
(2)函数![]() 在(-1,1)为单调函数.证明如下:
在(-1,1)为单调函数.证明如下:
任取![]() ,则
,则
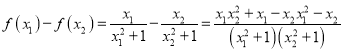

![]()
![]() ,
, ![]()
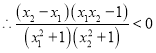
即![]()
故![]() 在(-1,1)上为增函数
在(-1,1)上为增函数
(3)由(1)、(2)可得
![]() 则
则
 解得:
解得: ![]()
所以,原不等式的解集为![]()
【点睛】
(1)奇偶性:判断与证明函数的奇偶性,首先要确定函数的定义域是否关于原点对称,再判断f(-x)与f(x)的关系,如果对定义域上的任意x,都满足f(-x)=f(x)就是偶函数,如果f(-x)=-f(x)就是奇函数,否则是非奇非偶函数。
(2)单调性:利函数单调性定义证明单调性,按假设,作差,化简,定号,下结论五个步骤。
【题型】解答题
【结束】
22
【题目】已知函数![]() .
.
(1)若![]() 的定义域和值域均是
的定义域和值域均是![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上是减函数,且对任意的
上是减函数,且对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,且对任意的
,且对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题: ①x0∈R,ln(x02+1)<0;
②x>2,x2>2x;
③α,β∈R,sin(α﹣β)=sin α﹣sin β;
④若q是¬p成立的必要不充分条件,则¬q是p成立的充分不必要条件.
其中真命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2017x+sin2017x,g(x)=log2017x+2017x , 则( )
A.对于任意正实数x恒有f(x)≥g(x)
B.存在实数x0 , 当x>x0时,恒有f(x)>g(x)
C.对于任意正实数x恒有f(x)≤g(x)
D.存在实数x0 , 当x>x0时,恒有f(x)<g(x)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查中小学课外使用互联网的情况,教育部向华东、华北、华南和西部地区60所中小学发出问卷![]() 份,
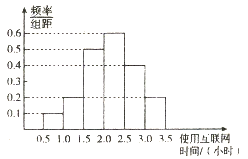
份, ![]() 名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
(1)要从这![]() 名中小学中用分层抽样的方法抽取
名中小学中用分层抽样的方法抽取![]() 名中小学生进一步调查,则在
名中小学生进一步调查,则在![]() (小时)时间段内应抽出的人数是多少?
(小时)时间段内应抽出的人数是多少?
(2)若希望![]() 的中小学生每天使用互联网时间不少于
的中小学生每天使用互联网时间不少于![]() (小时),请估计
(小时),请估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),当x≥0时,
f(x)= ,
,
则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
A.1﹣2a
B.2a﹣1
C.1﹣2﹣a
D.2﹣a﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】英格兰足球超级联赛,简称英超,是英国足球最高等级的职业足球联赛,也是世界最高水平的职业足球联赛之一,目前英超参赛球队有20个,在2014-2015赛季结束后将各队积分分成6段,并绘制出了如图所示的频率分布直方图(图中各分组区间包括左端点,不包括右端点,如第一组表示积分在[30,40)内).根据图中现有信息,解答下面问题:

(Ⅰ)求积分在[40,50)内的频率,并补全这个频率分布直方图;
(Ⅱ)从积分在[40,60)中的球队中任选取2个球队,求选取的2个球队的积分在频率分布直方图中处于不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为奇函数,当x≥0时,f(x)= ![]() .g(x)=
.g(x)= ![]() ,
,
(1)求当x<0时,函数f(x)的解析式,并在给定直角坐标系内画出f(x)在区间[﹣5,5]上的图象;(不用列表描点) 
(2)根据已知条件直接写出g(x)的解析式,并说明g(x)的奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[﹣2,t](t>﹣2)上的函数f(x)=(x2﹣3x+3)ex(其中e为自然对数的底).
(1)当t>1时,求函数y=f(x)的单调区间;
(2)设m=f(﹣2),n=f(t),求证:m<n;
(3)设g(x)=f(x)+(x﹣2)ex , 当x>1时,试判断方程g(x)=x的根的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com