
【题目】春季气温逐渐攀升,病菌滋生传播快,为了确保安全开学,学校按30名学生一批,组织学生进行某种传染病毒的筛查,学生先到医务室进行血检,检呈阳性者需到防疫部门]做进一步检测.学校综合考虑了组织管理、医学检验能力等多万面的因素,根据经验,采用分组检测法可有效减少工作量,具体操作如下:将待检学生随机等分成若干组,先将每组的血样混在一起化验,若结果呈阴性,则可断定本组血样合格,不必再做进一步的检测;若结果呈阳性,则本组中的每名学生再逐个进行检测.现有两个分组方案:方案一:将30人分成5组,每组6人;方案二:将30人分成6组,每组5人.已知随机抽一人血检呈阳性的概率为0.5%,且每个人血检是否呈阳性相互独立.
(Ⅰ)请帮学校计算一下哪一个分组方案的工作量较少?
(Ⅱ)已知该传染疾病的患病率为0.45%,且患该传染疾病者血检呈阳性的概率为99.9%,若检测中有一人血检呈阳性,求其确实患该传染疾病的概率.(参考数据:(![]() ,
,![]() )
)
【答案】(Ⅰ)方案一工作量更少.(Ⅱ)0.8991
【解析】
(Ⅰ)设方案一中每组的化验次数为X,则X的取值为1、7,分别求出相应的概率,求出![]() ,从而方案一的化验总次数的期望值为:
,从而方案一的化验总次数的期望值为:![]() 次.设方案二中每组的化验次数为Y,则Y的取值为1、6,分别求出相应的概率,求出
次.设方案二中每组的化验次数为Y,则Y的取值为1、6,分别求出相应的概率,求出![]() .从而方案二的化验总次数的期望为
.从而方案二的化验总次数的期望为![]() 次.由此能求出方案一工作量更少.
次.由此能求出方案一工作量更少.
(Ⅱ)设事件A:血检呈阳性,事件B:患疾病,由题意得![]() ,
,![]() ,
,![]() ,由此利用条件概率能求出该职工确实患该疾病的概率.
,由此利用条件概率能求出该职工确实患该疾病的概率.
解:(1)设方案一中每组的化验次数为X,则X的取值为1,7,
![]() ,
,
![]()
∴X的分布列为:
X | 1 | 7 |
P | 0.970 | 0.030 |
![]() .
.
故方案一的化验总次数的期望值为:![]() 次.
次.
设方案二中每组的化验次数为Y,则Y的取值为1,6,
![]() ,
,
![]() ,
,
∴Y的分布列为:
Y | 1 | 6 |
P | 0.975 | 0.025 |
![]() .
.
∴方案二的化验总次数的期望为![]() 次.
次.
∵![]() ,
,
∴方案一工作量更少.
(2)设事件A:血检呈阳性,事件B:患疾病,
则由题意得![]() ,
,![]() ,
,![]() ,
,
由条件概率公式![]() 可得
可得![]() ,
,
∴该职工确实患该疾病的概率![]() .
.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为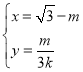 (
(![]() 为参数),设直线
为参数),设直线![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时点
变化时点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求出曲线![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
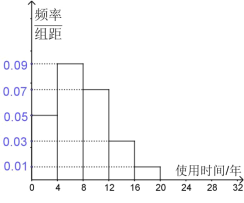
【题目】为了调查一款手机的使用时间,研究人员对该款手机进行了相应的测试,将得到的数据统计如下图所示:
并对不同年龄层的市民对这款手机的购买意愿作出调查,得到的数据如下表所示:
愿意购买该款手机 | 不愿意购买该款手机 | 总计 | |
40岁以下 | 600 | ||
40岁以上 | 800 | 1000 | |
总计 | 1200 |
(1)根据图中的数据,试估计该款手机的平均使用时间;
(2)请将表格中的数据补充完整,并根据表中数据,判断是否有99.9%的把握认为“愿意购买该款手机”与“市民的年龄”有关.
参考公式: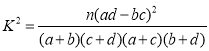 ,其中
,其中![]() .
.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式.孪生素数猜想是希尔伯特在二十世纪初提出的23个数学问题之一.可以这样描述:存在无穷多个素数![]() ,使得
,使得![]() 是素数,称素数对
是素数,称素数对![]() 为孪生素数.在不超过15的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( ).
为孪生素数.在不超过15的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() .
.
(Ⅰ)求曲线![]() 被直线
被直线![]() 截得的弦长;
截得的弦长;
(Ⅱ)与直线![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,求点
,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 对任意
对任意![]() 都有
都有![]() (其中
(其中![]() 、
、![]() 、
、![]() 是常数) .
是常数) .
(Ⅰ)当![]() ,
,![]() ,
,![]() 时,求
时,求![]() ;
;
(Ⅱ)当![]() ,
,![]() ,
,![]() 时,若
时,若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若数列![]() 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.当
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.当![]() ,
,![]() ,
,![]() 时,设
时,设![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() ,试问:是否存在这样的“封闭数列”,使得对任意
,试问:是否存在这样的“封闭数列”,使得对任意![]() ,都有
,都有![]() ,且
,且![]() .若存在,求数列
.若存在,求数列![]() 的首项
的首项![]() 的所有取值;若不存在,说明理由.
的所有取值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com