
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 根据条件,对$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{5}$两边平方便可求出${\overrightarrow{b}}^{2}$的值,进而求出$|\overrightarrow{b}|$的值.
解答 解:根据条件,
$(\overrightarrow{a}+\overrightarrow{b})^{2}={\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=$1+2+{\overrightarrow{b}}^{2}=5$;
∴${\overrightarrow{b}}^{2}=2$;
∴$|\overrightarrow{b}|=\sqrt{2}$.
故选B.
点评 考查数量积的运算,以及数量积的计算公式.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:选择题
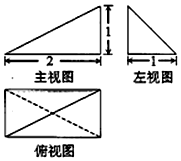
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
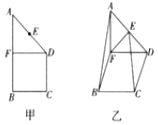 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com