
【题目】设![]() ,
, ![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)讨论![]() 在区间
在区间![]() 上的极值点个数;
上的极值点个数;
(3)是否存在![]() ,使得
,使得![]() 在区间
在区间![]() 上与
上与![]() 轴相切?若存在,求出所有
轴相切?若存在,求出所有![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)减区间为![]() ,增区间为
,增区间为![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】试题分析:(1)先求函数![]() 导数,再求导函数零点,列表分析导函数符号变化规律,确定单调区间(2)先求函数
导数,再求导函数零点,列表分析导函数符号变化规律,确定单调区间(2)先求函数![]() 导数,转化为研究
导数,转化为研究![]() 零点个数,利用二次求导易得
零点个数,利用二次求导易得![]() 在区间
在区间![]() 上单调递增,其零点个数决定于最小值的大小,讨论其最小值与零的大小得到极值点个数, (3)由题意得
上单调递增,其零点个数决定于最小值的大小,讨论其最小值与零的大小得到极值点个数, (3)由题意得![]() 在区间
在区间![]() 上与
上与![]() 轴相切切点为极值点
轴相切切点为极值点![]() ,由(2)得
,由(2)得![]() ,再根据极值点定义可得方程组
,再根据极值点定义可得方程组![]() ,解得
,解得![]()
试题解析:解:(1)当![]() 时:
时:![]() ,(
,(![]() )
)
故![]()
![]()
当![]() 时:
时:![]() ,当
,当![]() 时:
时:![]() ,当
,当![]() 时:
时:![]() .
.
故![]() 的减区间为:
的减区间为:![]() ,增区间为
,增区间为![]()
(2)![]()
令![]()
![]() ,故
,故![]() ,
,![]() ,
,
显然![]() ,又当
,又当![]() 时:
时:![]() .当
.当![]() 时:
时:![]() .
.
故![]()
![]() ,
,![]()
![]() ,
,![]() .
.
故![]() 在区间
在区间![]() 上单调递增,
上单调递增,
注意到:当![]() 时,
时,![]()
![]() ,故
,故![]() 在
在![]() 上的零点个数由
上的零点个数由![]() 的符号决定.
的符号决定.
①当![]() ,即:
,即:![]() 或
或![]() 时:
时:![]() 在区间
在区间![]() 上无零点,即
上无零点,即![]() 无极值点.
无极值点.
②当![]() ,即:
,即:![]() 时:
时:![]() 在区间
在区间![]() 上有唯一零点,即
上有唯一零点,即![]() 有唯一极值点.
有唯一极值点.
综上:当![]() 或
或![]() 时:
时:![]() 在
在![]() 上无极值点.
上无极值点.
当![]() 时:
时:![]() 在
在![]() 上有唯一极值点.
上有唯一极值点.
(3)假设存在![]() ,使得
,使得![]() 在区间
在区间![]() 上与
上与![]() 轴相切,则
轴相切,则![]() 必与
必与![]() 轴相切于极值点处,
轴相切于极值点处,
由(2)可知:![]() .不妨设极值点为
.不妨设极值点为![]() ,则有:
,则有:
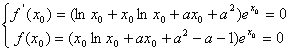 …(*)同时成立.
…(*)同时成立.
联立得:![]() ,即
,即![]() 代入(*)可得
代入(*)可得![]() .
.
令![]() ,
,![]() .
.
则![]() ,
,![]() ,当
,当 ![]() 时
时![]() (
(![]()
![]()
![]() 2).
2).
故![]() 在
在![]() 上单调递减.又
上单调递减.又![]() ,
, ![]() .
.
故![]() 在
在![]() 上存在唯一零点
上存在唯一零点![]() .
.
即当![]() 时
时![]() ,
,![]() 单调递增.当
单调递增.当![]() 时
时![]() ,
,![]() 单调递减.
单调递减.
因为![]() ,
,![]() .
.
故![]() 在
在![]() 上无零点,在
上无零点,在![]() 上有唯一零点.
上有唯一零点.
由观察易得![]() ,故
,故![]() ,即:
,即:![]() .
.
综上可得:存在唯一的![]() 使得
使得![]() 在区间
在区间![]() 上与
上与![]() 轴相切.
轴相切.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x|(x﹣a),a为实数.
(1)若函数f(x)为奇函数,求实数a的值;
(2)若函数f(x)在[0,2]为增函数,求实数a的取值范围;
(3)是否存在实数a(a<0),使得f(x)在闭区间 ![]() 上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x||x﹣a|≤3,x∈R},B={x|x2﹣3x﹣4>0,x∈R}.
(1)若a=1,求A∩B;
(2)若A∪B=R,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log3x.
(1)求f(45)﹣f(5)的值;
(2)若函数y=g(x)(x∈R)是奇函数,当x>0时,g(x)=f(x),求函数 y=g(x)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为整数的数列{an}满足an2≤1,1≤a12+a22+…+an2≤m,m,n∈N* .
(1)若m=1,n=2,写出所有满足条件的数列{an};
(2)设满足条件的{an}的个数为f(n,m).
①求f(2,2)和f(2016,2016);
②若f(m+1,m)>2016,试求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某影院为了宣传影片《战狼Ⅱ》,准备采用以下几种方式来扩大影响,吸引市民到影院观看影片,根据以往经验,预测:
①分发宣传单需要费用1.5万元,可吸引30%的市民,增加收入4万元;
②网络上宣传,需要费用8千元,可吸引20%的市民,增加收入3万元;
③制作小视频上传微信群,需要费用2.5万元,可吸引35%的市民,增加收入5.5万元;
④与商场合作需要费用1万元,购物满800元者可免费观看影片(商场购票),可吸收15%的市民,增加收入2.5万元,
问: (1)在三个观看影片的市民中,至少有一个是通过微信群宣传方式吸引来的概率是多少?
(2)影院预计可增加盈利是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆. 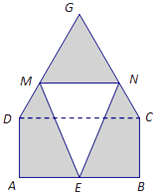
(1)设MN与AB之间的距离为x米,试将△EMN的面积S(平方米)表示成关于x的函数;
(2)求△EMN的面积S(平方米)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累积净化量![]() ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据![]() 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量![]() 有如下等级划分:
有如下等级划分:
累积净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器(共5000台)的质量,随机抽取![]() 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这![]() 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在![]() 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
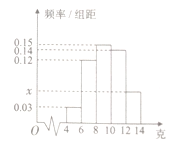
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累积净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com