
分析 (1)将函数解析式写出分段函数,然后作图;
(2)将函数解析式写出分段函数后,令每一段上均为单调减函数函数,且第一段最小值大于或大于第二段的最大值,或每一段上均为增函数,且第一段上最大值小于或等于第二段的最小值.
解答 解:(1)当a=0时,f(x)=|x+1|=$\left\{\begin{array}{l}{x+1,x≥-1}\\{-x-1,x<-1}\end{array}\right.$
作出函数图象如图: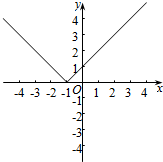
当a=2时,f(x)=$\left\{\begin{array}{l}{3x+1,x≥-1}\\{x-1,x<-1}\end{array}\right.$,
作出函数图象如图:
(2)f(x)=$\left\{\begin{array}{l}{(1+a)x+1,x≥-1}\\{(-1+a)x-1,x<-1}\end{array}\right.$.
①若f(x)是增函数,则$\left\{\begin{array}{l}{1+a>0}\\{-1+a>0}\\{-(1+a)+1≤-(-1+a)-1}\end{array}\right.$,
解得a>1.
②若f(x)是减函数,则$\left\{\begin{array}{l}{1+a<0}\\{-1+a<0}\\{-(1+a)+1≥-(-1+a)-1}\end{array}\right.$,
解得a<-1.
综上所述:实数a的取值范围是(-∞,-1)∪(1,+∞).
点评 本题考查了分段函数的图象和单调性,是中档题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x1)>f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)<f(x2) | D. | 无法比较f(x1)与f(x2)的大小 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 函数y=f(x)的部分图象如图所示,函数g(x)=sin(2x+φ)(0<φ<π)为偶函数,要得到g(x)的图象,只需将y=f(x)的图象向( )平移( )个单位.
函数y=f(x)的部分图象如图所示,函数g(x)=sin(2x+φ)(0<φ<π)为偶函数,要得到g(x)的图象,只需将y=f(x)的图象向( )平移( )个单位.| A. | 右:$\frac{π}{6}$ | B. | 左:$\frac{π}{6}$ | C. | 右:$\frac{π}{12}$ | D. | 左:$\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21,6,2 | B. | 7,1,2 | C. | 0,1,2 | D. | 0,6,6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+$\frac{4}{x}$ | B. | y=sinx+$\frac{4}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{{x}^{2}+2}{\sqrt{{x}^{2}+1}}$ | D. | y=$\sqrt{x}$+$\frac{9}{\sqrt{x}}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1<a<5 | B. | a≥5 | C. | 1<a≤5 | D. | a<5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com