
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,且过点
,且过点 ![]() .
. 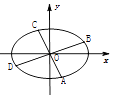
(1)求椭圆的标准方程;
(2)四边形ABCD的顶点在椭圆上,且对角线AC、BD过原点O,若 ![]() . (i) 求
. (i) 求 ![]() 的最值;
的最值;
(ii) 求四边形ABCD的面积.
【答案】
(1)解:由题意 ![]() ,
, ![]() ,又a2=b2+c2,
,又a2=b2+c2,
解得:a2=8,b2=4,
∴椭圆的标准方程为 ![]()
(2)解:设直线AB的方程为y=kx+m,再设A(x1,y1),B(x2,y2),
联立 ![]() ,得(1+2k2)x2+4kmx+2m2﹣8=0.
,得(1+2k2)x2+4kmx+2m2﹣8=0.
△=(4m)2﹣4(1+2k2)(2m2﹣8)=8(8k2﹣m2+4)>0…①
![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
,
![]()
= ![]() ,
,
∴ ![]() ,得4k2+2=m2.
,得4k2+2=m2.
(i) ![]() =
= ![]() .
.
∴﹣2=2﹣4 ![]() .
.
当k=0(此时m2=2满足①式),即直线AB平行于x轴时, ![]() 的
的
最小值为﹣2.
又直线AB的斜率不存在时, ![]() ,
,
∴ ![]() 的最大值为2;
的最大值为2;
(ii)设原点到直线AB的距离为d,则
![]()
= 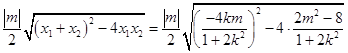
= ![]() .
.
∴ ![]()
【解析】(1)与已知列关于a,b,c的方程组,求解方程组可得a,b的值,则椭圆的标准方程可求;(2)设直线AB的方程为y=kx+m,联立直线方程和椭圆方程,由 ![]() 可得k与m的关系.(i)由数量积的坐标运算把
可得k与m的关系.(i)由数量积的坐标运算把 ![]() 化为含有k的代数式求得最值;(ii)首先求出△AOB的面积,乘以4即可求得四边形ABCD的面积.
化为含有k的代数式求得最值;(ii)首先求出△AOB的面积,乘以4即可求得四边形ABCD的面积.


科目:高中数学 来源: 题型:
【题目】下列数列中,既是递增数列又是无穷数列的是( )
A.1, ![]() ,
, ![]() ,
, ![]() ,…
,…
B.﹣1,﹣2,﹣3,﹣4,…
C.﹣1,﹣ ![]() ,﹣
,﹣ ![]() ,﹣
,﹣ ![]() ,…
,…
D.1, ![]() ,
, ![]() ,…,
,…, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形BCDE的边长为a,已知AB= ![]() BC,将△ABE沿边BE折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
BC,将△ABE沿边BE折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述: 
① AB与DE所成角的正切值是 ![]() ;
;
②AB∥CE
③VB﹣ACE体积是 ![]() a3;
a3;
④平面ABC⊥平面ADC.
其中正确的有 . (填写你认为正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3. 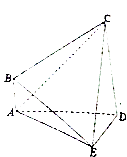
(1)求棱锥C﹣ADE的体积;
(2)在线段DE上是否存在一点P,使AF∥平面BCE?若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PC⊥平面ABC,∠ACB=45°,BC=2 ![]() ,AB=2.
,AB=2. 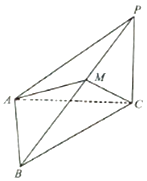
(1)求AC的长;
(2)若PC= ![]() ,点M在侧棱PB上,且
,点M在侧棱PB上,且 ![]() =
= ![]() ,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且asinAsinB+bcos2A= ![]() a.
a.
(1)求 ![]() ;
;
(2)若c2=a2+ ![]() b2 , 求角C.
b2 , 求角C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,已知对任意n∈N* , a1+a2+a3+…+an=3n﹣1,则a12+a22+a32+…+an2等于( )
A.(3n﹣1)2
B.![]()
C.9n﹣1
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com