
| A. | (x+2)2+(y-2)2=10 | B. | (x+2)2+(y-2)2=40 | C. | (x-2)2+(y+2)2=10 | D. | (x-2)2+(y+2)2=40 |
分析 因为线段AB为所求圆的直径,所以利用中点坐标公式求出线段AB的中点即为所求圆的圆心坐标,再利用两点间的距离公式求出圆心C与点A之间的距离即为所求圆的半径,根据求出的圆心坐标与半径写出圆的标准方程即可.
解答 解:∵A(1,3),B(-5,1),设圆心为C,
∴圆心C的坐标为C(-2,2);
∴|AC|=$\sqrt{10}$,即圆的半径r=$\sqrt{10}$,
则以线段AB为直径的圆的方程是(x+2)2+(y-2)2=10.
故选A.
点评 此题考查了中点坐标公式,两点间的距离公式以及圆的标准方程,解答本题的关键是灵活运用已知条件确定圆心坐标及圆的半径.同时要求学生会根据圆心与半径写出圆的标准方程.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
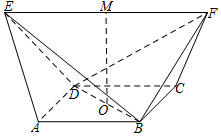 如图,在五面体ABCDEF中,底面ABCD是正方形,△ADE,△BCF都是等边三角形,EF∥AB,且EF>AB,M,O分别为EF,BD的中点,连接MO.
如图,在五面体ABCDEF中,底面ABCD是正方形,△ADE,△BCF都是等边三角形,EF∥AB,且EF>AB,M,O分别为EF,BD的中点,连接MO.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
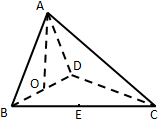 如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{7}}{8}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com