
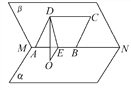
【题目】如图,已知二面角α-MN-β的大小为60°,菱形ABCD在平面β内,A,B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥平面α,垂足为O.
(1)证明:AB⊥平面ODE.
(2)求异面直线BC与OD所成角的余弦值.
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:(1)由DO⊥α,ABα,所以DO⊥AB,连接BD,可得DE⊥AB,由线面垂直的判定定理即可证得成立;(2) 因为BC∥AD,所以BC与OD所成的角等于AD与OD所成的角,即∠ADO是BC与OD所成的角. 由(1)知,AB⊥平面ODE,所以AB⊥OE,又DE⊥AB,∠DEO是二面角α-MN-β的平面角,从而∠DEO=60°, 不妨设AB=2,则AD=2,在Rt△DOE中求出DO的长度,作比求出余弦值,即可求出答案.
试题解析:
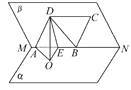
(1)如图,因为DO⊥α,ABα,所以DO⊥AB,连接BD,由题设知,△ABD是正三角形,又E是AB的中点,所以DE⊥AB,DO∩DE=D,故AB⊥平面ODE.
(2)因为BC∥AD,所以BC与OD所成的角等于AD与OD所成的角,即∠ADO是BC与OD所成的角.
由(1)知,AB⊥平面ODE,所以AB⊥OE,又DE⊥AB,于是∠DEO是二面角α-MN-β的平面角,从而∠DEO=60°.
不妨设AB=2,则AD=2,易知DE=![]() .
.
在Rt△DOE中,DO=DE·sin60°=![]() ,
,
连接AO,在Rt△AOD中,cos∠ADO=![]() =
=![]() =
=![]() ,
,
故异面直线BC与OD所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() x3﹣(1+
x3﹣(1+ ![]() )x2+2bx在区间[3,5]上不是单调函数,则函数f(x)在R上的极大值为( )
)x2+2bx在区间[3,5]上不是单调函数,则函数f(x)在R上的极大值为( )
A.![]() b2﹣
b2﹣ ![]() b3
b3
B.![]() b﹣
b﹣ ![]()
C.0
D.2b﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
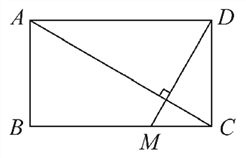
【题目】如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,给出以下四个结论:
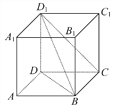
①D1C∥平面A1ABB1;②A1D1与平面BCD1相交;
③AD⊥平面D1DB;④平面BCD1⊥平面A1ABB1.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年存节期间,某服装超市举办了一次有奖促销活动,消费每超过600 元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种. 方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸到2个红球,则打6折;若摸到1个红球,则打7折;若没摸到红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了 600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
天数/天 | 151~180 | 181~210 | 211~240 | 241~270 | 271~300 | 301~330 | 331~360 | 361~390 |
灯管数/只 | 1 | 11 | 18 | 20 | 25 | 16 | 7 | 2 |
(1)试估计这种日光灯的平均使用寿命;
(2)若定期更换,可选择多长时间统一更换合适?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com